✅ Week 02 Lab - Solutions

2024/25 Autumn Term

Author

Stuart Bramwell & Tabtim Duenger & Yassine Lahna

Published

07 Oct 2024

This solution file follows the format of the Quarto file .qmd you had to fill in during the lab session. If you want to render the document yourselves and play with the code, you can download the .qmd version of this solution file by clicking on the button below:

📋 Lab Tasks

🛠 Part I: Data manipulation with `dplyr` (40 min)

⚙️ Setup

Import required libraries:

library(ggsci)       # for nice colour themes
library(psymetadata) # imports meta-analyses in psychology
library(tidyverse)

Try this option if having issues with the imports above

library(dplyr)       # for data manipulation
library(tidyr)       # for data reshaping
library(readr)       # for reading data
library(tidyselect)  # for selecting columns
library(ggsci)       # for nice colour themes
library(psymetadata) # imports meta-analyses in psychology

No need to load any data here: we can already have access to the meta-analyses by loading psymetadata. Let’s proceed! 😉

1.3. Let’s print the Gnambs (2020) study on the colour red and cognitive performance to inspect it (to read the study click here).


gnambs2020

   es_id study_id          author pub_year country color   n  design          yi         vi
1      1        1      arthur2016     2016      US green  76 between  0.42962966 0.05399213
2      2        1      arthur2016     2016      US green 164 between  0.02241093 0.02439540
3      3        1      arthur2016     2016      US green  87 between  0.08424910 0.04602388
4      4        2    bertrams2015     2015      DE  gray  33 between  0.04243733 0.12135082
5      5        2    bertrams2015     2015      DE  gray  38 between  0.36195605 0.10727940
6      6        3    caschera2015     2015      US green  16 between -0.40603799 0.25515209
7      7        3    caschera2015     2015      US green  16 between -1.06405824 0.28538187
8      8        4     castell2018     2018      DE white  87 between -0.15592584 0.04612282
9      9        4     castell2018     2018      DE  blue  82 between  0.05975972 0.04891862
10    10        4     castell2018     2018      DE white  87 between  0.62738053 0.04824519
11    11        4     castell2018     2018      DE  blue  82 between  0.24486849 0.04926245
12    12        5    drummond2017     2017      US green  61 between -0.53809445 0.06796472
13    13        5    drummond2017     2017      US black  80 between -0.09004085 0.05005067
14    14        6      elliot2007     2007      US green  46 between -0.08153267 0.08974087
15    15        6      elliot2007     2007      US black  44 between -0.20421041 0.09310546
16    16        6      elliot2007     2007      DE green  30 between -1.24221480 0.15905163
17    17        6      elliot2007     2007      DE white  31 between -0.99518508 0.14514075
18    18        6      elliot2007     2007      DE green  22 between -1.50566649 0.23485678
19    19        6      elliot2007     2007      DE  gray  18 between -0.75788046 0.24095508
20    20        6      elliot2007     2007      DE green  40 between -0.52792523 0.10449391
21    21        6      elliot2007     2007      DE  gray  35 between -0.47919619 0.11765950
22    22        7      elliot2019     2019      US green  40  within  0.09816078 0.10012044
23    23        7      elliot2019     2019      US green 135  within  0.10710784 0.02967374
24    24        8      gnambs2010     2010      AT green 131 between -0.51065384 0.03153143
25    25        8      gnambs2010     2010      DE  blue 133 between -0.03721585 0.03021875
26    26        8      gnambs2010     2010      DE  blue 128 between -0.07885028 0.03165265
27    27        9      gnambs2015     2015      AT  gray  97 between -0.09021946 0.04131855
28    28       10     hulshof2013     2013      NL  blue 122 between -0.36350974 0.03333725
29    29       11     larsson2015     2015      UK green 185 between -0.11950249 0.02184435
30    30       11     larsson2015     2015      UK green 187 between -0.10166396 0.02155653
31    31       11     larsson2015     2015      UK green 187 between -0.04280798 0.02153380
32    32       11     larsson2015     2015      UK green 187 between  0.02817422 0.02153102
33    33       11     larsson2015     2015      UK green 187 between  0.08502521 0.02154823
34    34       12       maier2008     2008      DE  gray  20 between -1.36525072 0.24659774
35    35       12       maier2008     2008      DE  gray  22 between -0.95957841 0.20274524
36    36       13      pedley2016     2016      UK  blue  42 between  0.01800906 0.09524196
37    37       13      pedley2016     2016      UK green  42 between  0.16483926 0.09556157
38    38       13      pedley2016     2016      UK  gray  42 between -0.36178666 0.09679630
39    39       13      pedley2016     2016      UK  blue  88 between  0.05403447 0.04547113
40    40       13      pedley2016     2016      UK green  88 between  0.15787682 0.04559617
41    41       13      pedley2016     2016      UK  blue  30 between  0.61282103 0.13959249
42    42       13      pedley2016     2016      UK green  30 between  0.27583259 0.13460139
43    43       13      pedley2016     2016      UK  gray  30 between  0.38843495 0.13584803
44    44       13      pedley2016     2016      UK white  32 between -1.22135442 0.14830792
45    45       13      pedley2016     2016      UK green  30 between  0.21855065 0.13412941
46    46       13      pedley2016     2016      UK white  30 between  0.49173897 0.13736345
47    47       14         shi2015     2015      CN  blue  58 between -0.56622416 0.07172939
48    48       15      smajic2014     2014      US green 137 between -0.15571391 0.02928713
49    49       15      smajic2014     2014      US  blue  31 between  0.02065594 0.13248551
50    50       15      smajic2014     2014      US green  32 between -0.01510595 0.12698769
51    51       15      smajic2014     2014      US white  30 between  0.08862273 0.13901979
52    52       15      smajic2014     2014      US  blue  25 between  0.44648793 0.16632469
53    53       15      smajic2014     2014      US green  24 between  0.10958691 0.17167876
54    54       15      smajic2014     2014      US white  20 between  0.21923470 0.23929683
55    55       16      steele2015     2015      US  gray 206 between -0.11662028 0.01945049
56    56       16      steele2015     2015      US green 203 between  0.07272187 0.01971794
57    57       17      steele2016     2016      US  gray 163 between -0.05925117 0.02455157
58    58       17      steele2016     2016      US green 188 between -0.04358281 0.02128165
59    59       18      steele2017     2017      US  gray 266 between -0.07336750 0.01504771
60    60       18      steele2017     2017      US green 246 between -0.01016984 0.01626037
61    61       19      steele2018     2018      US  gray 282 between -0.01069011 0.01418460
62    62       19      steele2018     2018      US green 277 between -0.07549990 0.01445091
63    63       20 thorstenson2015     2015      US green  82 between -0.47312263 0.05014540
64    64       20 thorstenson2015     2015      US  gray  86 between -0.37206302 0.04741730
65    65       21     vukovic2017     2017      RS black  96 between  0.07110487 0.04169300
66    66       21     vukovic2017     2017      RS green  95 between  0.16987675 0.04226181
67    67       22       zhang2014     2014      CN green  24 between -1.10909168 0.19229342

1.4. As you can see, printing gnambs2020 results in the whole contents of the data frame being printed out.

⚠️ Do not make a habit out of this.

Printing whole data frames is too much information and can severely detract from the overall flow of the document. Remember that, at the end of the day, data scientists must be able to effectively communicate their work to both technical and non-technical users, and it impresses no-one when whole data sets (particularly extremely large ones!) are printed out. Instead, we can print tibbles which are a data frame with special properties.


gnambs2020 %>% 
  as_tibble()

# A tibble: 67 × 10
   es_id study_id author       pub_year country color     n design       yi     vi
   <int>    <int> <chr>           <int> <chr>   <chr> <int> <chr>     <dbl>  <dbl>
 1     1        1 arthur2016       2016 US      green    76 between  0.430  0.0540
 2     2        1 arthur2016       2016 US      green   164 between  0.0224 0.0244
 3     3        1 arthur2016       2016 US      green    87 between  0.0842 0.0460
 4     4        2 bertrams2015     2015 DE      gray     33 between  0.0424 0.121 
 5     5        2 bertrams2015     2015 DE      gray     38 between  0.362  0.107 
 6     6        3 caschera2015     2015 US      green    16 between -0.406  0.255 
 7     7        3 caschera2015     2015 US      green    16 between -1.06   0.285 
 8     8        4 castell2018      2018 DE      white    87 between -0.156  0.0461
 9     9        4 castell2018      2018 DE      blue     82 between  0.0598 0.0489
10    10        4 castell2018      2018 DE      white    87 between  0.627  0.0482
# ℹ 57 more rows
# ℹ Use `print(n = ...)` to see more rows

Note that we can tell the dimensions of the data (r nrow(gnambs2020) rows and r ncol(gnambs2020) columns) and can see the first ten rows and however many columns can fit into the R console. This is a much more compact way of introducing a data frame.

Try it out:

 nrow(gnambs2020)

[1] 67

 ncol(gnambs2020)

[1] 10

For the majority of these labs, we will work with tibbles instead of base R data frames. This is not only because they have a nicer output when we print them, but also because we can do advanced things like create list columns (more on this later).

1.5. We can further inspect the data frame using the glimpse() function from the dplyr package. This can be especially useful when you have lots of columns, as printing tibbles typically only shows as many columns that can fit into the R console.


gnambs2020 %>%
  glimpse()

Rows: 67
Columns: 10
$ es_id    <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26,…
$ study_id <int> 1, 1, 1, 2, 2, 3, 3, 4, 4, 4, 4, 5, 5, 6, 6, 6, 6, 6, 6, 6, 6, 7, 7, 8, 8, 8, 9, 10, 11, 11, 1…
$ author   <chr> "arthur2016", "arthur2016", "arthur2016", "bertrams2015", "bertrams2015", "caschera2015", "cas…
$ pub_year <int> 2016, 2016, 2016, 2015, 2015, 2015, 2015, 2018, 2018, 2018, 2018, 2017, 2017, 2007, 2007, 2007…
$ country  <chr> "US", "US", "US", "DE", "DE", "US", "US", "DE", "DE", "DE", "DE", "US", "US", "US", "US", "DE"…
$ color    <chr> "green", "green", "green", "gray", "gray", "green", "green", "white", "blue", "white", "blue",…
$ n        <int> 76, 164, 87, 33, 38, 16, 16, 87, 82, 87, 82, 61, 80, 46, 44, 30, 31, 22, 18, 40, 35, 40, 135, …
$ design   <chr> "between", "between", "between", "between", "between", "between", "between", "between", "betwe…
$ yi       <dbl> 0.42962966, 0.02241093, 0.08424910, 0.04243733, 0.36195605, -0.40603799, -1.06405824, -0.15592…
$ vi       <dbl> 0.05399213, 0.02439540, 0.04602388, 0.12135082, 0.10727940, 0.25515209, 0.28538187, 0.04612282…

1.6. 👥 DISCUSS IN PAIRS/GROUPS: Time to switch to another study. Type ?barroso2021 in the console. What columns are in the Barroso et al (2021) study? What is this study about?

1.7. Let’s explore another study again. Let’s take a look at the Maldonado et al (2020) study which explores age differences in executive function.


maldonado2020 %>% 
  as_tibble()

# A tibble: 1,268 × 13
   es_id study_id author        domain           n1    n2 n_total mean_age1 mean_age2 miyake task      yi      vi
   <int>    <int> <chr>         <chr>         <int> <int>   <int> <chr>     <chr>     <chr>  <chr>  <dbl>   <dbl>
 1     1        1 Aguirre, 2014 updating         48    48      96 20.5      68.31     no     Volu…  0.871 2.29e+0
 2     2        2 Balouch, 2013 shifting         28    29      57 24.64     67.86     no     Trai… -0.258 7.19e-2
 3     3        2 Balouch, 2013 processing s…    28    29      57 24.64     67.86     no     Digi…  1.53  9.80e-1
 4     4        2 Balouch, 2013 updating         28    29      57 24.64     67.86     no     Tea …  0.396 1.14e-1
 5     5        3 Barulli, 2013 shifting         20    18      38 24.7      68.2      no     Shif…  2.73  3.45e+4
 6     6        4 Bernard, 2013 shifting         10    16      26 21.7      61.9      no     Trai…  1.25  1.94e+0
 7     7        4 Bernard, 2013 updating         10    16      26 21.7      61.9      no     Ster…  2.00  8.24e+1
 8     8        4 Bernard, 2013 processing s…    10    16      26 21.7      61.9      no     Choi…  0.671 4.12e+2
 9     9        5 Brand, 2013   updating        251    46     297 24.55     70.35     no     Dice…  0.428 1.63e-1
10    10        5 Brand, 2013   shifting        251    46     297 24.55     70.35     yes    Modi…  0.782 5.39e-2
# ℹ 1,258 more rows
# ℹ Use `print(n = ...)` to see more rows

As you can see, the study includes different domains (remember to look at ?maldonado2020). We can see how different domains are included in the meta-analysis and the number of studies that focus on each domain by using the count function.


maldonado2020 %>% 
  as_tibble() %>% 
  count(domain)

# A tibble: 4 × 2
  domain               n
  <chr>            <int>
1 inhibition         289
2 processing speed   270
3 shifting           208
4 updating           501

Suppose we only wanted to compare effect sizes and variances for the “updating” domain. We can employ the filter verb to do this. How many rows do you think will be in this data frame?


maldonado2020 %>% 
  as_tibble() %>% 
  filter(domain == "updating")

# A tibble: 501 × 13
   es_id study_id author          domain      n1    n2 n_total mean_age1 mean_age2 miyake task          yi     vi
   <int>    <int> <chr>           <chr>    <int> <int>   <int> <chr>     <chr>     <chr>  <chr>      <dbl>  <dbl>
 1     1        1 Aguirre, 2014   updating    48    48      96 20.5      68.31     no     Voluntary… 0.871  2.29 
 2     4        2 Balouch, 2013   updating    28    29      57 24.64     67.86     no     Tea Task   0.396  0.114
 3     7        4 Bernard, 2013   updating    10    16      26 21.7      61.9      no     Sternberg… 2.00  82.4  
 4     9        5 Brand, 2013     updating   251    46     297 24.55     70.35     no     Dice Task  0.428  0.163
 5    11        5 Brand, 2013     updating   251    46     297 24.55     70.35     no     Iowa Gamb… 0.766  2.45 
 6    15        9 Cavallini, 2013 updating    30    29      59 23.63     74.99     no     Dual Task  2.00   0.916
 7    16        9 Cavallini, 2013 updating    30    29      59 23.63     74.99     no     Verbal Fl… 1.78   1.01 
 8    22       13 Gorlick, 2013A  updating    37    30      67 21.74     66.87     no     Rule Lear… 0.147  0.856
 9    23       14 Gorlick, 2013B  updating    34    31      65 21.88     67.35     no     Rule Lear… 0.143  0.877
10    31       19 Mathias, 2013   updating    63    15      78 24.67     69.13     no     Progressi… 1.44   0.151
# ℹ 491 more rows
# ℹ Use `print(n = ...)` to see more rows

1.8. Now, let’s look at the Nuijten et al (2020) study on intelligence. Suppose we were only interested in the unique study ID, effect size and variance. We can select these columns which produces a data frame with a reduced number of columns.


nuijten2020 %>% 
  as_tibble() %>% 
  select(study_id, yi, vi)

# A tibble: 2,443 × 3
   study_id    yi      vi
      <dbl> <dbl>   <dbl>
 1       32 0.371 0.00267
 2      636 0.390 0.0122 
 3     1267 0.603 0.00855
 4     1182 0.658 0.00296
 5     1901 0.324 0.00495
 6     1124 0.231 0.00253
 7     1027 0.386 0.00297
 8      837 0.514 0.00467
 9       22 0.469 0.0189 
10     1069 0.688 0.0156 
# ℹ 2,433 more rows
# ℹ Use `print(n = ...)` to see more rows

Sometimes, you may want to change variable names to make them more descriptive. yi and vi may not be helpful, so we can change them to something like effect_size and effect_variance by using the rename function.


nuijten2020 %>% 
  as_tibble() %>% 
  select(study_id, yi, vi) %>% 
  rename(effect_size = yi, effect_variance = vi)

# A tibble: 2,443 × 3
   study_id effect_size effect_variance
      <dbl>       <dbl>           <dbl>
 1       32       0.371         0.00267
 2      636       0.390         0.0122 
 3     1267       0.603         0.00855
 4     1182       0.658         0.00296
 5     1901       0.324         0.00495
 6     1124       0.231         0.00253
 7     1027       0.386         0.00297
 8      837       0.514         0.00467
 9       22       0.469         0.0189 
10     1069       0.688         0.0156 
# ℹ 2,433 more rows
# ℹ Use `print(n = ...)` to see more rows

Note: you can also rename columns by citing their relative position in the data frame.


nuijten2020 %>% 
  as_tibble() %>% 
  select(study_id, yi, vi) %>% 
  rename(effect_size = 2, effect_variance = 3)

# A tibble: 2,443 × 3
   study_id effect_size effect_variance
      <dbl>       <dbl>           <dbl>
 1       32       0.371         0.00267
 2      636       0.390         0.0122 
 3     1267       0.603         0.00855
 4     1182       0.658         0.00296
 5     1901       0.324         0.00495
 6     1124       0.231         0.00253
 7     1027       0.386         0.00297
 8      837       0.514         0.00467
 9       22       0.469         0.0189 
10     1069       0.688         0.0156 
# ℹ 2,433 more rows
# ℹ Use `print(n = ...)` to see more rows

1.9. Now let’s create a new variable. We’ll do this with the Agadullina et al (2018) meta-analysis on out-group entitativity and prejudice. Suppose we want to see how many effect sizes are statistically significant. We can calculate t-values by dividing the effect size by the square root of the effect variance (a.k.a. the standard error). To do this, we can use the mutate function to create a new variable effect_tvalue.

👨🏻‍🏫 TEACHING MOMENT: Your tutor will briefly explain a succinct way of understanding t-values.


agadullina2018 %>% 
  as_tibble() %>% 
  # Let's use some of the code in the previous subsection
  select(study_id, yi, vi) %>% 
  rename(effect_size = yi, effect_variance = vi) %>% 
  mutate(effect_tvalue = effect_size / sqrt(effect_variance))

# A tibble: 85 × 4
   study_id effect_size effect_variance effect_tvalue
      <int>       <dbl>           <dbl>         <dbl>
 1        1       0.814         0.00526         11.2 
 2        1       0.228         0.00526          3.14
 3        1       0.521         0.00526          7.18
 4        1       0.657         0.00526          9.05
 5        2      -0.383         0.0118          -3.53
 6        2      -0.189         0.0118          -1.74
 7        2       0.492         0.00339          8.46
 8        2       0.209         0.00171          5.05
 9        2       0.212         0.00171          5.13
10        2      -0.485         0.00180        -11.4 
# ℹ 75 more rows
# ℹ Use `print(n = ...)` to see more rows

Now that we have created a new column, we may want to calculate some summary statistics. For example, we can ask how big the t-values are, on average. We can pipe in the summarise command to calculate this average. (Note: we want to take the average of the absolute values, so we need to use the abs function wrapped inside mean.)


# We copy and paste the code in the above chunk ...
agadullina2018 %>% 
  as_tibble() %>% 
  select(study_id, yi, vi) %>% 
  rename(effect_size = yi, effect_variance = vi) %>% 
  mutate(effect_tvalue = effect_size / sqrt(effect_variance)) %>%
# ... and pipe in summarise
  summarise(effect_tvalue = mean(abs(effect_tvalue)))

# A tibble: 1 × 1
  effect_tvalue
          <dbl>
1          6.07

1.10 As a final part, suppose we think that there may be average differences in t-values based on the design of the study. Agadullina et al (2018) have data from both cross-sectional observational studies and experiments. We can tweak our pipeline to calculate group means based on design by using the group_by function.


agadullina2018 %>% 
  as_tibble() %>% 
  # Remember to select the design column
  select(study_id, yi, vi, design) %>% 
  rename(effect_size = yi, effect_variance = vi) %>% 
  mutate(effect_tvalue = effect_size / sqrt(effect_variance)) %>%
  group_by(design) %>% 
  summarise(effect_tvalue = mean(abs(effect_tvalue)))

# A tibble: 2 × 2
  design          effect_tvalue
  <chr>                   <dbl>
1 Cross-sectional          6.74
2 Experiment               2.66

We can see that, on average, the effects of cross-sectional studies are r round(6.74/2.66, 1) times more precisely estimated! We’ll explore this discrepancy graphically in the next part of this lab.

📋 Part 2: Data visualisation with `ggplot`(50 min)

They say a picture paints a thousand words, and we are, more often than not, inclined to agree with them (whoever “they” are)! Thankfully, we can use perhaps the most widely used package, ggplot2 (click here for documentation) to paint such pictures or (more accurately) build such graphs.

2.1 Histograms

Suppose we want to plot the distribution of an outcome of interest. We can use a histogram to plot the effect sizes found in Nuijten et al (2020).

Tip

📝 Note: Step-by-step

If you are not familiar with using ggplot for plotting, the line by line construction of the plot below might be useful. The + operator is used to add layers to the plot.


nuijten2020 %>% 
  as_tibble() %>% 
  ggplot(aes(es)) +
  geom_histogram()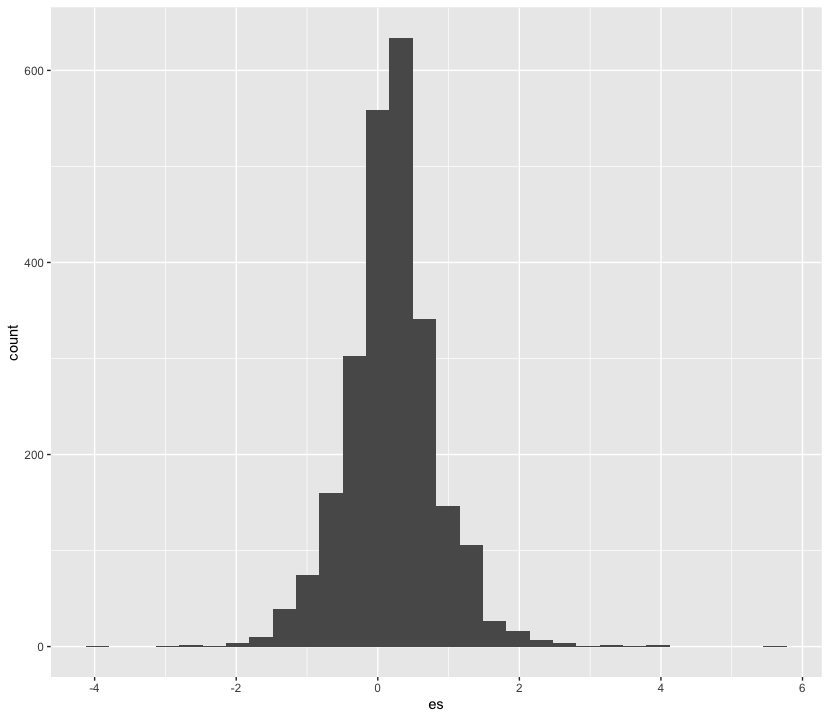

👥 WORK IN PAIRS/GROUPS:

Include the following custom theme:


theme_histogram <- function() {
  
  theme_minimal() +
  theme(panel.grid.minor = element_blank(),
        panel.grid.major.x = element_blank())
  
}

Change a few parameters in the geom_histogram layer. Set
bins to 100
colour to “black”
fill to “lightgrey”
alpha to 0.5

#modify your code here
nuijten2020 %>% 
  as_tibble() %>% 
  ggplot(aes(es)) +
  geom_histogram(bins = 100, colour = "black", fill = "lightgrey", alpha = 0.5) +
  theme_histogram() +
  labs(x = "Effect sizes in Nuijten et al (2020)", y = "Count")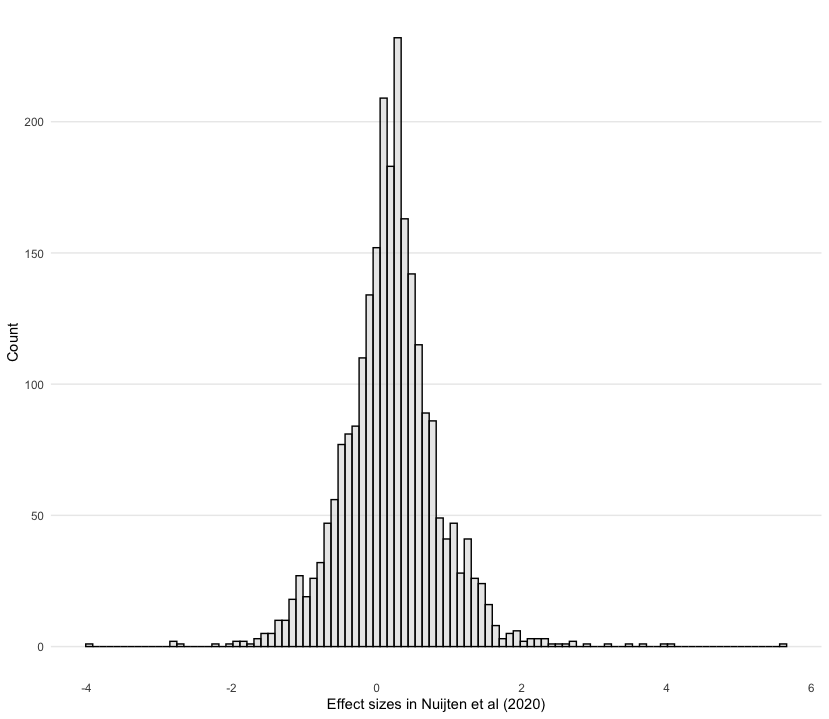

🗣️ CLASSROOM DISCUSSION:

Are there any alterations to this graph that would make it better?

2.2 Bar graphs

We counted the number of studies in the Maldonado et al (2020) meta analysis that featured different domains. We can use ggplot to create a bar graph. We first need to specify what we want on the x and y axes, which constitute the first and second argument of the aes function.


maldonado2020 %>% 
  as_tibble() %>% 
  count(domain, name = "n_studies") %>% 
  ggplot(aes(n_studies, domain)) +
  geom_col()

👥 WORK IN PAIRS/GROUPS:

Include the following custom theme:


theme_bar <- function() {
  
  theme_minimal() +
  theme(panel.grid.minor = element_blank(),
        panel.grid.major.y = element_blank())
  
}

Edit the axes. Use “Number of studies” on the x-axis and “Domain” on the y-axis by adding the labs function.
Check out the fct_reorder function to order the domains by the number of studies. You can do this in a separate mutate line or in the aes wrapper.


maldonado2020 %>% 
  as_tibble() %>% 
  count(domain, name = "n_studies") %>% 
  mutate(domain = fct_reorder(domain, n_studies)) %>% 
  ggplot(aes(n_studies, domain)) +
  geom_col() +
  theme_bar() +
  labs(x = "Number of studies", y = "Domain")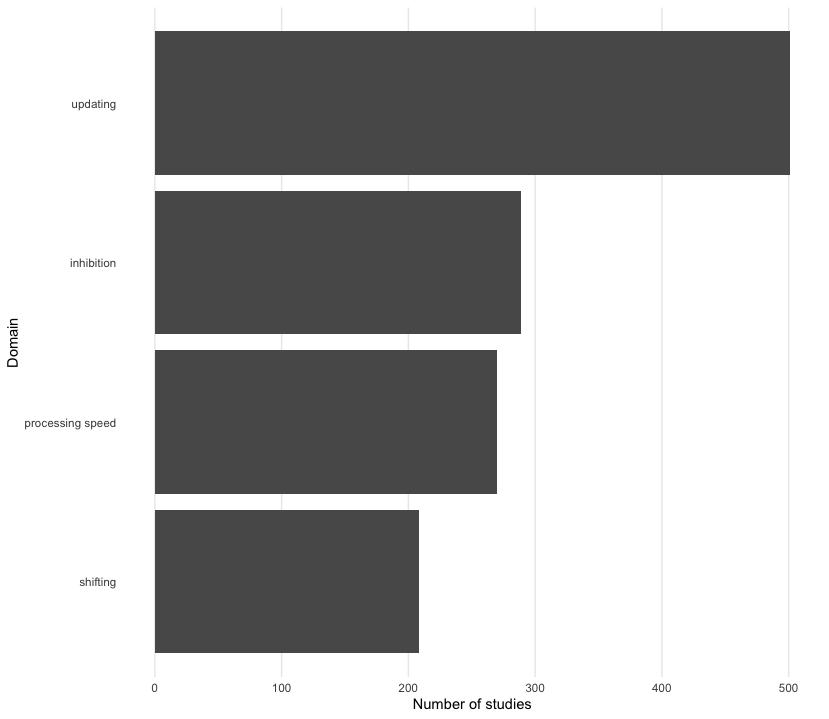

👉 NOTE: Don’t like horizontal bars? Well, we can also create vertical bars too. Can you guess how we code this?

2.3 Scatter plots

Scatter plots are the best way to graphically summarise the relationship between two quantitative variables. Suppose we wanted to track effect sizes and statistical significance on intelligence studies found in Nuijten et al. (2020). We can use a scatter plot to visualise this, distinguishing effect sizes by whether or not they achieve conventional levels of significance (p < 0.05) using colour.


nuijten2020 %>% 
  as_tibble() %>% 
  drop_na(yi) %>% 
  ggplot(aes(year, yi, colour = abs(yi / sqrt(vi)) > 1.96)) +
  geom_point()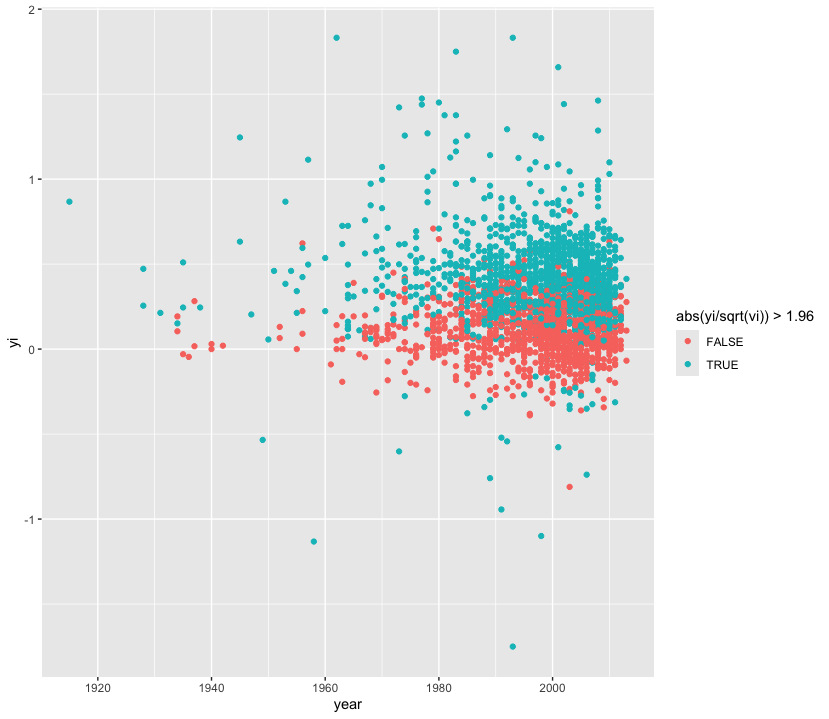

👥 WORK IN PAIRS/GROUPS:

Include the following custom theme:

theme_scatter <- function() {
  
  theme_minimal() +
  theme(panel.grid.minor = element_blank(),
        legend.position = "bottom")
  
}

Only include studies from 1980 onward.
Include a horizontal dashed line using geom_hline.
It is hard to see the number of studies, try these two things:
Replace geom_point with geom_jitter.
Try adding translucency to each point.
Replace the colour scheme (try scale_colour_cosmic())
Label the x-axis with “Year”, the y-axis with “Effect sizes in Nuijten et al. (2020)”, and colour with “Statistically significant?”


nuijten2020 %>% 
  as_tibble() %>% 
  drop_na() %>% 
  filter(year >= 1980) %>% 
  ggplot(aes(year, yi, colour = abs(yi / sqrt(vi)) > 1.96)) +
  geom_hline(yintercept = 0, linetype = "dashed") +
  geom_jitter(alpha = 0.5) +
  theme_scatter() +
  scale_colour_cosmic() +
  labs(x = "Year", y = "Effect sizes in Nuijten et al. (2020)", colour = "Statistically significant?")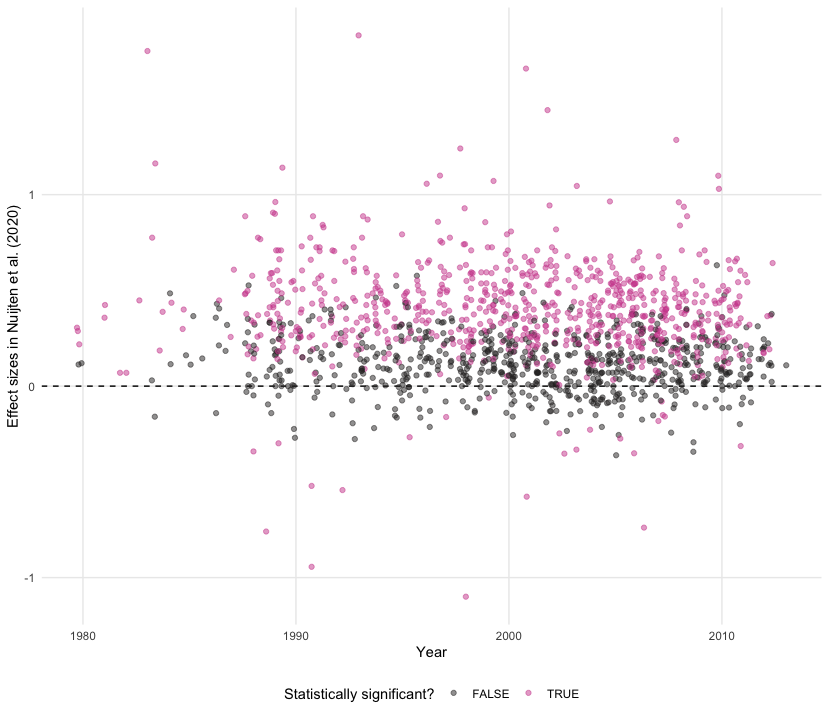

2.4 Line plots

Line plots can be used to track parameters of interest over time. With Nuijten et al (2020), we can see how many studies were included in their meta-analysis over time.

nuijten2020 %>% 
  as_tibble() %>% 
  count(year) %>% 
  ggplot(aes(year, n)) +
  geom_line()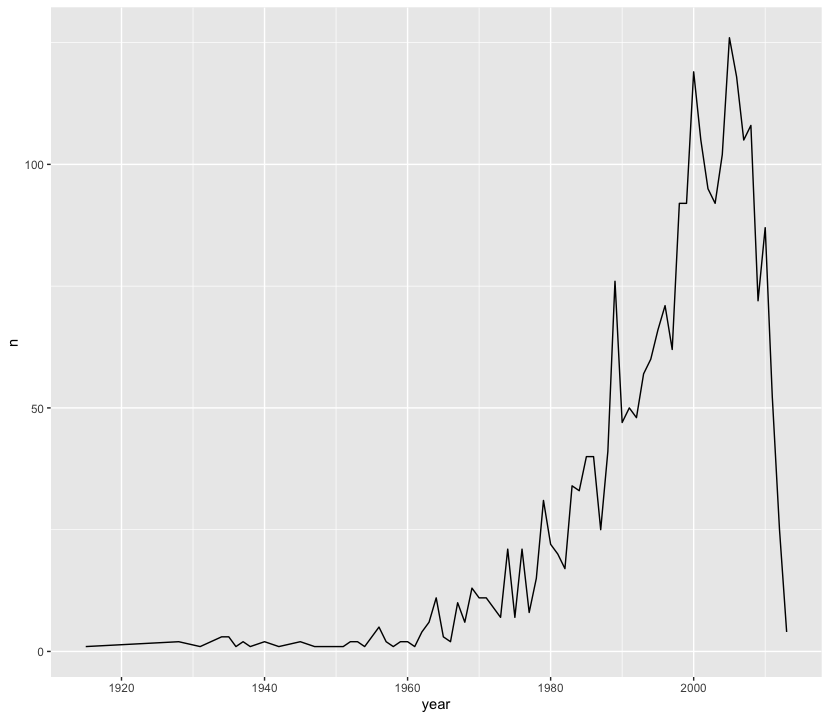

👥 WORK IN PAIRS/GROUPS:

Include the following custom theme:

theme_line <- function() {
  
  theme_minimal() +
  theme(panel.grid.minor = element_blank(),
        panel.grid.major.x = element_blank())
  
}

Change layer from a line to an area (note: this may not be suitable in all cases)
Fill the area in “midnightblue” and set the alpha to 0.5
Capitalise the x-axis and change the y-axis to “Number of studies”


nuijten2020 %>% 
  as_tibble() %>% 
  count(year) %>% 
  ggplot(aes(year, n)) +
  geom_area(fill = "midnightblue", alpha = 0.5) +
  theme_line() +
  labs(x = "Year", y = "Number of Studies in Nuijten (2020)")

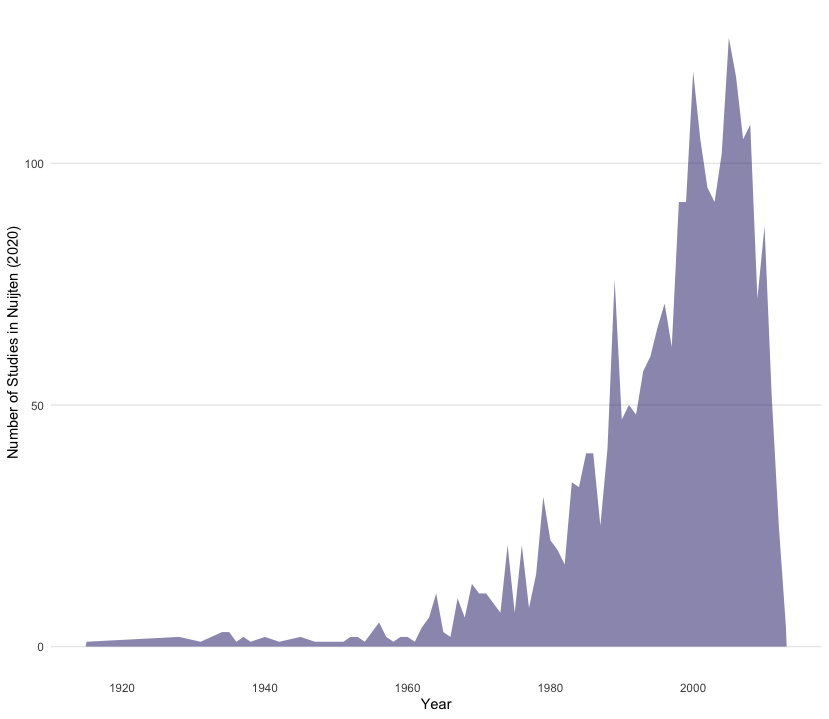
👉 NOTE: We think this line plot works in this context, and that it is useful to introduce you to this style of charting progress over time. However, for others contexts filling the area under the line may not work, so do bear this in mind when making decisions!

2.5 Box plots

Box plots are an excellent way to summarise the distribution of values across different strata over key quantities of interest (e.g. median, interquartile range). Recall that Agadullina et al (2018) code whether or not a study is cross-sectional or experimental and that we found average discrepancies in terms of significance levels between these two strata. We can use box plots to graphically illustrate this.


agadullina2018 %>% 
  as_tibble() %>% 
  mutate(ti = abs(yi / sqrt(vi))) %>% 
  ggplot(aes(design, ti, fill = design)) +
  geom_boxplot()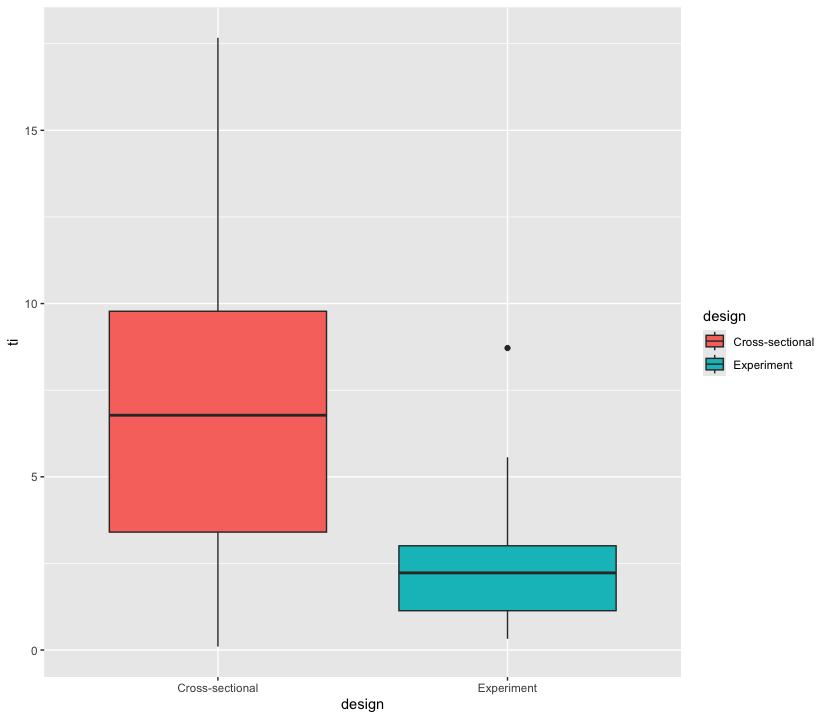

👥 WORK IN PAIRS/GROUPS:

Include the following custom theme:

theme_boxplot <- function() {
  
  theme_minimal() +
  theme(panel.grid = element_blank(),
        legend.position = "none")
  
}

Add scale_fill_bmj()
Set the alpha values in the box plot layer to 0.75
Set the x-axis label to NULL and y-axis to “T-values in Agadullina et al (2018)”


agadullina2018 %>% 
  as_tibble() %>% 
  mutate(ti = abs(yi / sqrt(vi))) %>% 
  ggplot(aes(design, ti, fill = design)) +
  geom_boxplot(alpha = 0.75) +
  theme_boxplot() +
  scale_fill_bmj() +
  labs(x = NULL, y = "T-values in Agadullina et al (2018)")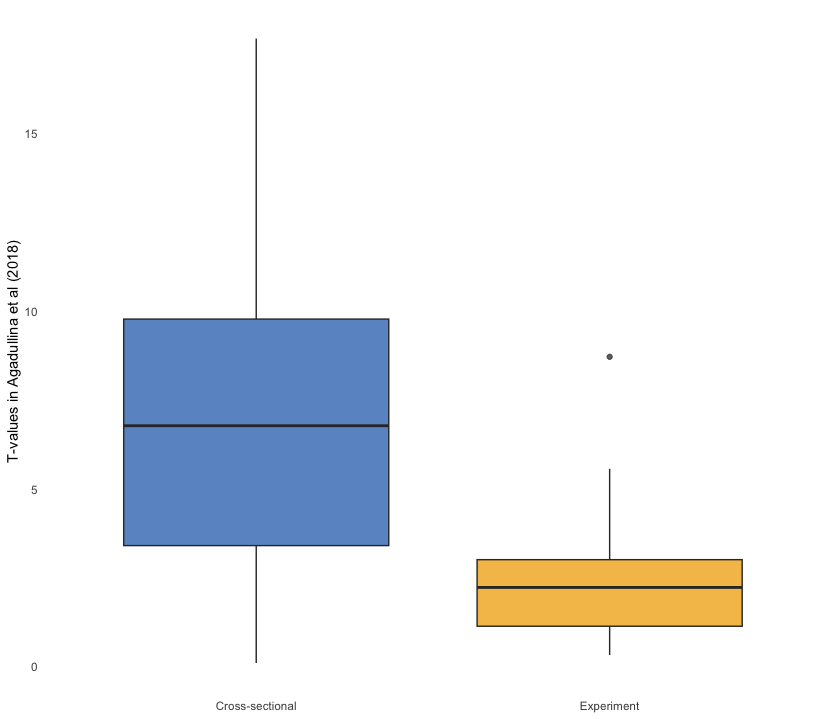

2.6 Density plots

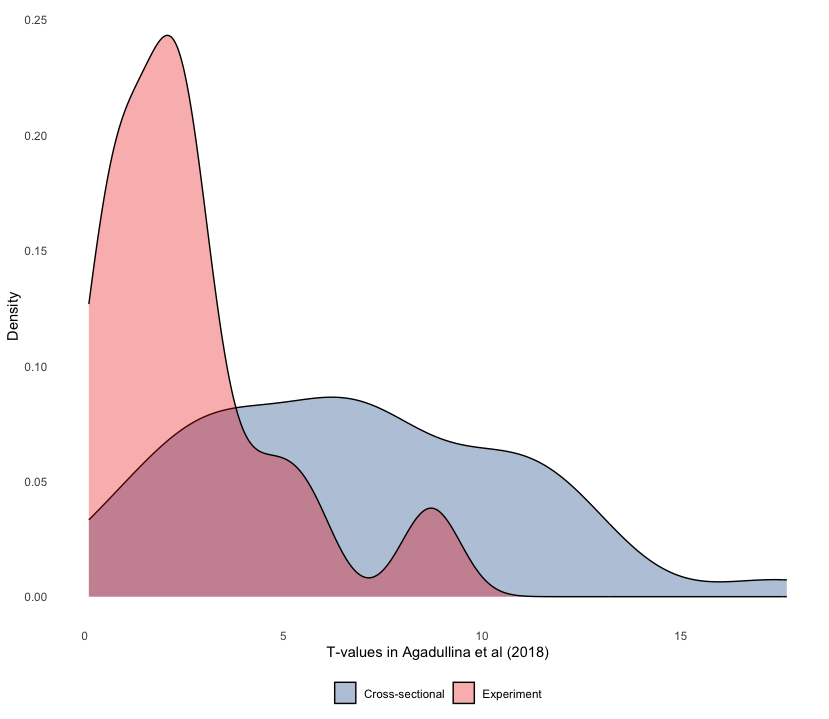
Let’s look at another way of showing discrepancies found in Agadullina et al (2018), namely density plots. Although we cannot see quantities of interest, we can get a better sense of how t-values are distributed across different strata in a more raw manner.


agadullina2018 %>% 
  as_tibble() %>% 
  mutate(ti = yi / sqrt(vi)) %>% 
  ggplot(aes(abs(ti), fill = design)) +
  geom_density()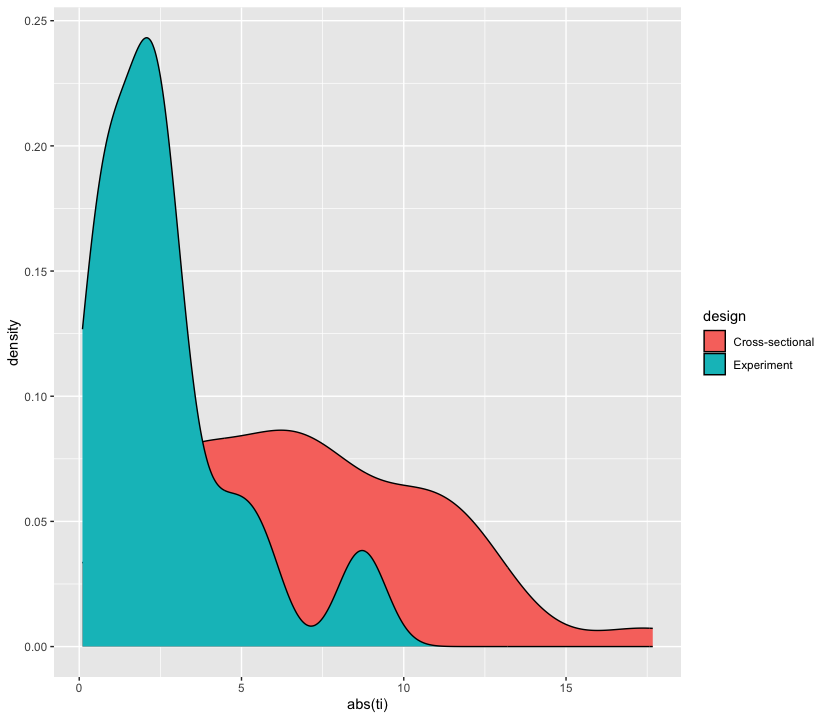

👥 WORK IN PAIRS/GROUPS:

Include the following custom theme:

theme_density <- function() {
  
  theme_minimal() +
  theme(panel.grid = element_blank(),
        legend.position = "bottom")
  
}

Add scale_fill_lancet()
Set the alpha values in the density layer to 0.75
Set the x-axis label to “T-values in Agadullina et al (2018)” and y-axis to “Density”

agadullina2018 %>% 
  as_tibble() %>% 
  mutate(ti = yi / sqrt(vi)) %>% 
  ggplot(aes(abs(ti), fill = design)) +
  geom_density(alpha = 0.325) +
  theme_density() +
  scale_fill_lancet() +
  labs(x = "T-values in Agadullina et al (2018)", y = "Density",
       fill = NULL)

📋 Lab Tasks

🛠 Part I: Data manipulation with dplyr (40 min)

⚙️ Setup

📋 Part 2: Data visualisation with ggplot(50 min)

2.1 Histograms

2.2 Bar graphs

2.3 Scatter plots

2.4 Line plots

2.5 Box plots

2.6 Density plots

🛠 Part I: Data manipulation with `dplyr` (40 min)

📋 Part 2: Data visualisation with `ggplot`(50 min)