✅ Week 03 Lab - Solutions
2023/24 Autumn Term
Instead of just reading the solutions, you might want to download the .qmd file and run the code yourself. You can download the .qmd file by clicking on the download button below:
⚙️ Setup
Import required libraries:
# Remember to install.packages() any missing packages using the Console
library(dplyr)
library(readr)
library(lubridate)
library(tidymodels)Read the data set:
It is the same data set you used in the previous lab (as well as in the first formative assignment):
# Modify the filepath if needed
filepath <- "data/UK-HPI-full-file-2023-06.csv"
uk_hpi <- read_csv(filepath)Rows: 136935 Columns: 54
── Column specification ────────────────────────────────────────────────────────
Delimiter: ","
chr (3): Date, RegionName, AreaCode
dbl (51): AveragePrice, Index, IndexSA, 1m%Change, 12m%Change, AveragePriceS...
ℹ Use `spec()` to retrieve the full column specification for this data.
ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.Pre-process the dataset:
# Replicate roughly the same steps you did in the previous lab:
# 1. Select the columns you need
# 2. Rename the columns
# 3. Filter the data set to include only the regions you need (let's focus on England for now)
# 4. Preprocess the date column
selected_cols <- c("Date", "RegionName", "12m%Change")
df_england <-
uk_hpi %>%
select(all_of(selected_cols)) %>%
rename(date = Date, region = RegionName, yearly_change = `12m%Change`) %>%
filter(region == "England") %>%
drop_na(yearly_change) %>%
mutate(date = lubridate::dmy(date))
df_england %>% head(8) %>% knitr::kable()| date | region | yearly_change |
|---|---|---|
| 1969-04-01 | England | 6.250000 |
| 1969-05-01 | England | 6.250000 |
| 1969-06-01 | England | 6.250000 |
| 1969-07-01 | England | 4.395604 |
| 1969-08-01 | England | 4.395604 |
| 1969-09-01 | England | 4.395604 |
| 1969-10-01 | England | 5.524862 |
| 1969-11-01 | England | 5.524862 |
Add lagged variables:
# Add lagged variables for the dependent variable
df_england <-
df_england %>%
arrange(date) %>% # Sort in ascending order so we can use lag later
mutate(yearly_change_lag1 = lag(yearly_change, 1)) %>%
drop_na() %>%
arrange(desc(date)) # sort by date in descending order just to make it easier to read📋 Lab Tasks
Part I - the lm command (25 min)
👨🏻🏫 TEACHING MOMENT: Your class teacher will demonstrate how to run the lm function.
Task 1: Run a linear regression model with yearly_change as the dependent variable and yearly_change_lag1 as the independent variable. Save the model as model1.
model1 <- lm(yearly_change ~ yearly_change_lag1, data = df_england)Print the model summary:
summary(model1)Call:
lm(formula = yearly_change ~ yearly_change_lag1, data = df_england)
Residuals:
Min 1Q Median 3Q Max
-11.8994 -0.2940 0.0037 0.3715 12.3700
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.136960 0.095864 1.429 0.154
yearly_change_lag1 0.984141 0.007039 139.803 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.825 on 648 degrees of freedom
Multiple R-squared: 0.9679, Adjusted R-squared: 0.9679
F-statistic: 1.954e+04 on 1 and 648 DF, p-value: < 2.2e-16🗣️ DISCUSSION:
- What is the value of the intercept?
\(\approx 0.137\)
- What is the value of the slope?
\(\approx 0.984\)
- How should you interpret this model?
The relationship is fairly 1:1, as expected. For every one percentage point increase in the
yearly_changein house prices as measured in the previous month, we forecast a 0.984 percentage point increase in this month’s house price change.If the model is a good fit, we can also expect the slope to be correct within a 95% confidence interval of 0.984 +/- 0.007 (given by the Std. Error of the slope coefficient).
👨🏻🏫 TEACHING MOMENT: Your class teacher will demonstrate how to plot the model.
Task 2: Plot the residuals against the fitted values.
plot(model1, 1)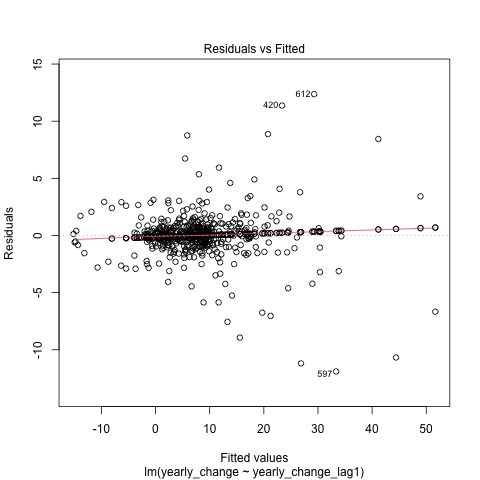
Alternatively, see all four basic lm diagnostic plots:
par(mfrow = c(2, 2))
plot(model1)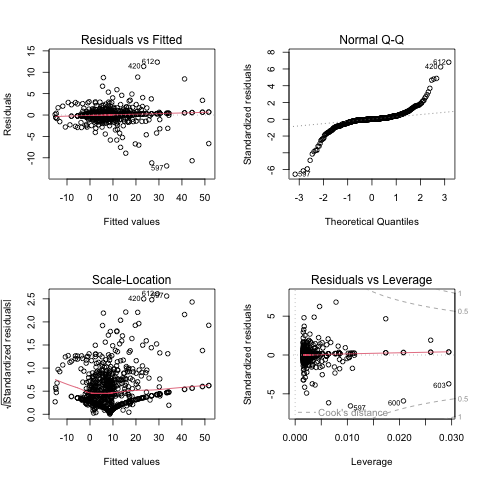
🗣️ DISCUSSION:
Is this a good fit? Why? Why not?
It seems like a good fit overall. However, the residual plot reveals a slight curvature, suggesting the relationship is not perfectly linear.
Part II - the tidymodels way (20 min)
👨🏻🏫 TEACHING MOMENT: Your class teacher will demonstrate how to get the same thing done using the tidymodels framework.
Task 3: Run a linear regression model with yearly_change as the dependent variable and yearly_change_lag1 as the independent variable. Save the model as model2.
model2 <-
linear_reg() %>%
set_engine("lm") %>%
fit(yearly_change ~ yearly_change_lag1, data = df_england)Print the model coefficients in a tidy way:
model2 %>% tidy()# A tibble: 2 × 5
term estimate std.error statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) 0.137 0.0959 1.43 0.154
2 yearly_change_lag1 0.984 0.00704 140. 0 See the full model summary:
model2$fit %>% summary()Call:
stats::lm(formula = yearly_change ~ yearly_change_lag1, data = data)
Residuals:
Min 1Q Median 3Q Max
-11.8994 -0.2940 0.0037 0.3715 12.3700
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.136960 0.095864 1.429 0.154
yearly_change_lag1 0.984141 0.007039 139.803 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.825 on 648 degrees of freedom
Multiple R-squared: 0.9679, Adjusted R-squared: 0.9679
F-statistic: 1.954e+04 on 1 and 648 DF, p-value: < 2.2e-16Overall statistics:
model2 %>% glance()# A tibble: 1 × 12
r.squared adj.r.squared sigma statistic p.value df logLik AIC BIC
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 0.968 0.968 1.83 19545. 0 1 -1312. 2631. 2644.
# ℹ 3 more variables: deviance <dbl>, df.residual <int>, nobs <int>Task 4: Augument the model with the residuals and the fitted values and use the resulting data frame to plot the residuals against the fitted values.
model2 %>% augment(df_england)# A tibble: 650 × 6
date region yearly_change yearly_change_lag1 .pred .resid
<date> <chr> <dbl> <dbl> <dbl> <dbl>
1 2023-06-01 England 1.9 1.7 1.81 0.0900
2 2023-05-01 England 1.7 3.2 3.29 -1.59
3 2023-04-01 England 3.2 3.6 3.68 -0.480
4 2023-03-01 England 3.6 5.2 5.25 -1.65
5 2023-02-01 England 5.2 6 6.04 -0.842
6 2023-01-01 England 6 8.5 8.50 -2.50
7 2022-12-01 England 8.5 9.9 9.88 -1.38
8 2022-11-01 England 9.9 11.4 11.4 -1.46
9 2022-10-01 England 11.4 8.6 8.60 2.80
10 2022-09-01 England 8.6 12 11.9 -3.35
# ℹ 640 more rowsThen use ggplot2 to plot the residuals against the fitted values:
ggplot(model2 %>% augment(df_england), aes(.pred, .resid)) +
geom_point()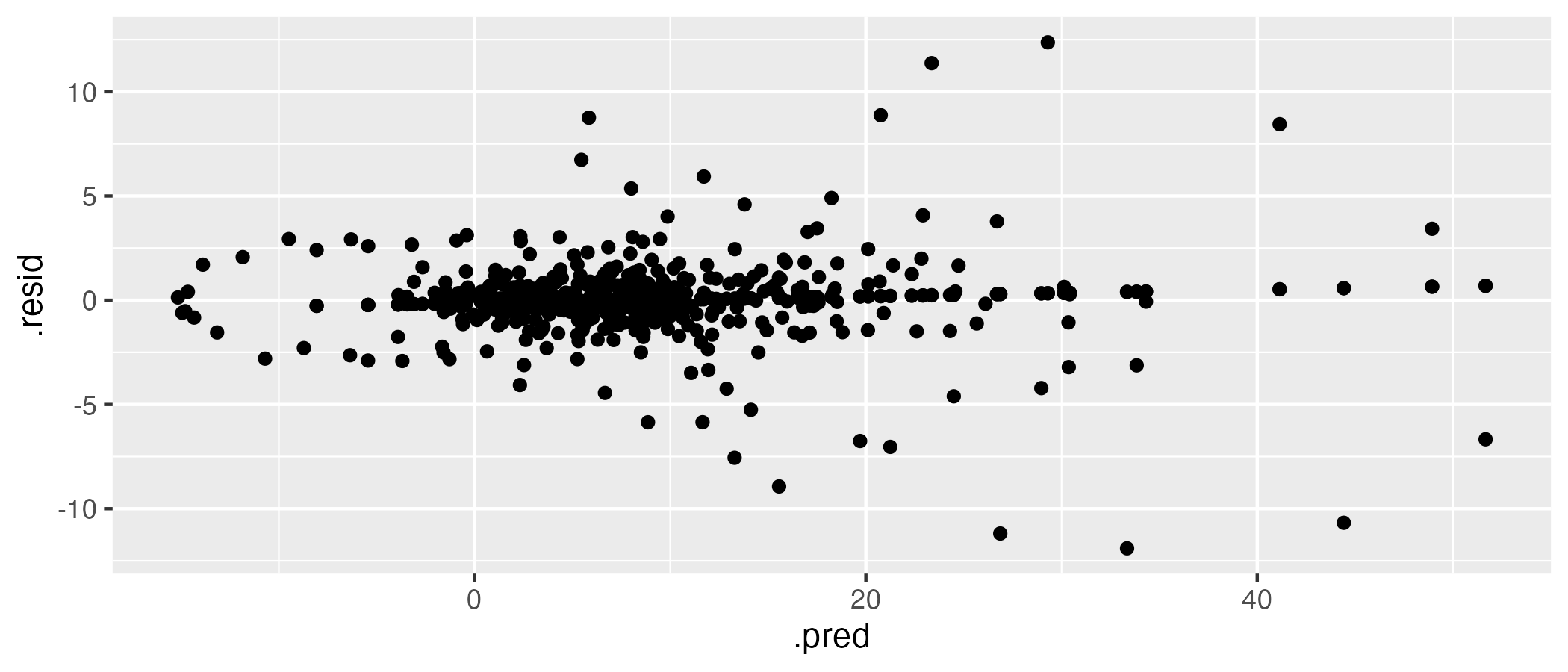
You can further customise the plot:
plot_df <- model2 %>% augment(df_england)
g <- ggplot(plot_df, aes(x = .pred, y = .resid)) +
geom_point(alpha=0.2, size=3, color="red", stroke=1) +
geom_hline(yintercept = 0, linetype = "dashed") +
labs(x = "Fitted values", y = "Residuals", title="Residuals vs Fitted") +
theme_bw() +
theme(axis.title.x = element_text(size = rel(1.2)),
axis.text.x = element_text(size = rel(1.2)),
axis.title.y = element_text(size = rel(1.2)),
axis.text.y = element_text(size = rel(1.2)),
plot.title = element_text(size = rel(1.5), face = "bold"))
g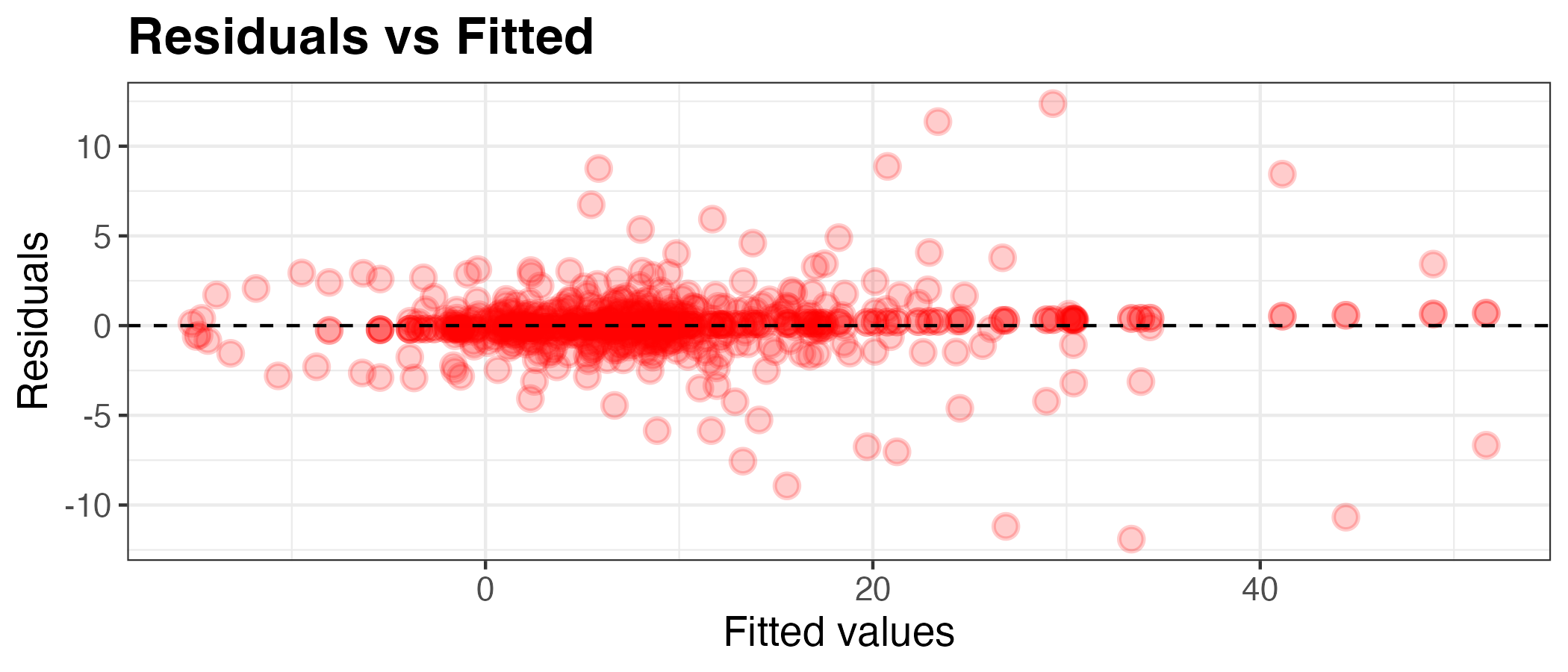
Part III - evaluating the model
STEP 01
- Separate the data into training and testing sets. The training set must contain data up until Dec 2020. The testing set must contain data from Jan 2021 onwards.
The reasoning here is as follows:
- I need to split my data into two separate data frames.
- The questions specifies what it calls ‘training set’ as all the data up until Dec 2020.
- Since we are subsetting the data by selecting rows, we can use the
filterfunction to select the rows we need. - To make date comparisons, it is imperative that all date objects and columns are stored as proper date objects.
- I have already properly modified the data type of the
datecolumn using lubridate. Therefore, I don’t need to modify anything else in that column. - However, I need to convert the string of text
"2021-01-01"to a proper date object. I can use lubridate’symdfunction to convert a string to a date object. - Great, now I can use the
filterfunction to select the rows I need.
df_england_train <- df_england %>% filter(date < ymd("2021-01-01"))
df_england_test <- df_england %>% filter(date >= ymd("2021-01-01"))Why do you need to convert date-related columns and objects to a date object using lubridate? The original data set has date in the format “DD/MM/YYYY” as a string. If you try to compare strings, you will get the wrong result because the comparison is done lexicographically (i.e. by alphabetical order).
For example, the following code will return TRUE, implying that 1 January 2021 happens before 1 December 2020:
"01/01/2021" < "01/12/2020"[1] TRUESTEP 02
- Fit a linear regression model with
tidymodelsusing just the training set. Call itmodel3. How does this model compare to the one you fitted in Part II?
How would you reason about this?
- I need to fit a linear regression model using
tidymodels. That is, copying the code from Part II (not withlm()). - I need to modify just the source of the data. Instead of using the entire data set, I need to use just the training set I created in STEP 01.
model3 <-
linear_reg() %>%
set_engine("lm") %>%
fit(yearly_change ~ yearly_change_lag1, data = df_england_train)In terms of comparison, if I tidy up the output of this new model, I will notice that it is very similar to the one we fitted in Part II. The coefficients are almost identical:
model3 %>% tidy()# A tibble: 2 × 5
term estimate std.error statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) 0.130 0.0931 1.39 0.164
2 yearly_change_lag1 0.986 0.00674 146. 0 STEP 03
- Calculate the Mean Absolute Error (MAE) for the training set. That is, on average, how far off is the model from the actual data?
How would you reason about this?
- I don’t know what the MAE is. I need to look it up.
- I go to the tidymodels website and search for “MAE” and “Mean Absolute Error”
- The results didn’t exactly showed me how to calculate the MAE. I wonder if there is something in one of the packages that are part of tidymodels.
- Eventually, you should find the
yardstickpackage. You can read the documentation of themae()function here. - From the documentation of the
mae()function, I look at the examples and deduce that I need to compare the model predictions with the actual values used to fit it. - I can use the
augment()function to get the predictions of the model on the training set. Then I can use themae()function to calculate the MAE.
model3 %>%
augment(df_england_train) %>%
mae(truth = yearly_change, estimate = .pred)# A tibble: 1 × 3
.metric .estimator .estimate
<chr> <chr> <dbl>
1 mae standard 0.848I am just printing out the value, but - alternatively - I can save it in a variable if I need to use it later:
mae_train <-
model3 %>%
augment(df_england_train) %>%
mae(truth = yearly_change, estimate = .pred)
mae_train# A tibble: 1 × 3
.metric .estimator .estimate
<chr> <chr> <dbl>
1 mae standard 0.848The MAE is approximately 0.848 percentage points. That means on average, the model is off by 0.848 percentage points.
STEP 04
- Calculate the Mean Absolute Error (MAE) for the testing set. That is, on average, how far off is the model from the actual data?
Here is when things start to get interesting. How would you reason about this?
- I have already trained a model,
model3on two variables:yearly_changeandyearly_change_lag1. - This means I can use the model to predict the
yearly_changefor any given value ofyearly_change_lag1, on any data set – it does not have to be the same data I used to train the model. - Therefore, I can use the
augment()function to get the predictions of the model on the testing set. Then I can use themae()function to calculate the MAE, just the same way I did before.
model3 %>%
augment(df_england_test) %>%
mae(truth = yearly_change, estimate = .pred)# A tibble: 1 × 3
.metric .estimator .estimate
<chr> <chr> <dbl>
1 mae standard 2.14OH WOW! This is a much higher error than the one we got for the training set. The model is on average wrong twice as much as it was on the training set. This can happen for many reasons: it could be that the model is so attuned to the training set that it is not able to generalise to the testing set, or it could mean that something changed in the dynamics that produced this data, and the model – fitted on older data – is not able to capture it. Which one do you think it is?
💡 A common source of confusion in this question was that many people assumed that we would have to train a new model. That is not the case, and this is the beauty of modelling. Once you have a model, you can use it to predict the outcome on any data set, as long as the data set has the same variables as the ones you used to train the model. (We will explore more of the implications and limitations of thinking this way in the future, in this course)
STEP 05
- Now create a
df_scotlandwith the same variables asdf, but only for Scotland (no need to separate into training and testing sets).
I can use the same code I used to create df_england in the beginning of this lab, but I need to change the filter condition to select only Scotland:
df_scotland <-
uk_hpi %>%
select(all_of(selected_cols)) %>%
rename(date = Date, region = RegionName, yearly_change = `12m%Change`) %>%
filter(region == "Scotland") %>%
drop_na(yearly_change) %>%
mutate(date = lubridate::dmy(date)) %>%
arrange(date) %>%
mutate(yearly_change_lag1 = lag(yearly_change, 1)) %>%
drop_na() %>%
arrange(desc(date))Notice that, different to what I did in the beginning of this lab, I did the filtering and created the lagged variable in the same pipe. Now that I am familiar with what I need to do, I don’t need to break it in multiple steps.
Checkin that it is correct:
df_scotland %>% head(8)# A tibble: 8 × 4
date region yearly_change yearly_change_lag1
<date> <chr> <dbl> <dbl>
1 2023-06-01 Scotland 0 1.9
2 2023-05-01 Scotland 1.9 1.4
3 2023-04-01 Scotland 1.4 2.2
4 2023-03-01 Scotland 2.2 1.8
5 2023-02-01 Scotland 1.8 0.6
6 2023-01-01 Scotland 0.6 4.5
7 2022-12-01 Scotland 4.5 5.6
8 2022-11-01 Scotland 5.6 6.6Further sanity check:
df_scotland$region %>% unique() # Retrieve all unique values in the `region` column[1] "Scotland"STEP 06
- How well can
model3predict monthly changes in house prices in Scotland?
Now that you have realised that model3 can be used in any dataset, you can use it to predict the monthly changes in house prices in Scotland the same way you did for the England test set. We can also calculate the MAE so we can compare it with the MAE we calculated for the England test set.
model3 %>%
augment(df_scotland) %>%
mae(truth = yearly_change, estimate = .pred)# A tibble: 1 × 3
.metric .estimator .estimate
<chr> <chr> <dbl>
1 mae standard 1.47The error is also higher, on average, than the one we got for the England training set. This is not surprising, since the model was trained on England data, and Scotland is a different country with different dynamics.
(Extra) Out of curiosity, we could see if the MAE changes over time. I could group the data by year and calculate the MAE for each year:
model3 %>%
augment(df_scotland) %>%
group_by(year = lubridate::year(date)) %>%
mae(yearly_change, .pred) # MAE is already a summary statistics, so I don't need to use summarise()While I am at it, I can plot it:
plot_df <-
model3 %>%
augment(df_scotland) %>%
group_by(year = lubridate::year(date)) %>%
mae(yearly_change, .pred)
g <-
(
ggplot(plot_df, aes(x=year, y=.estimate, color=.metric))
+ geom_line()
+ geom_point()
+ ylim(c(0, NA)) # Ensure the Y axis starts at zero. NA means "whatever the maximum value is"
+ labs(x = "Year", y = "MAE", title="MAE over time")
)
g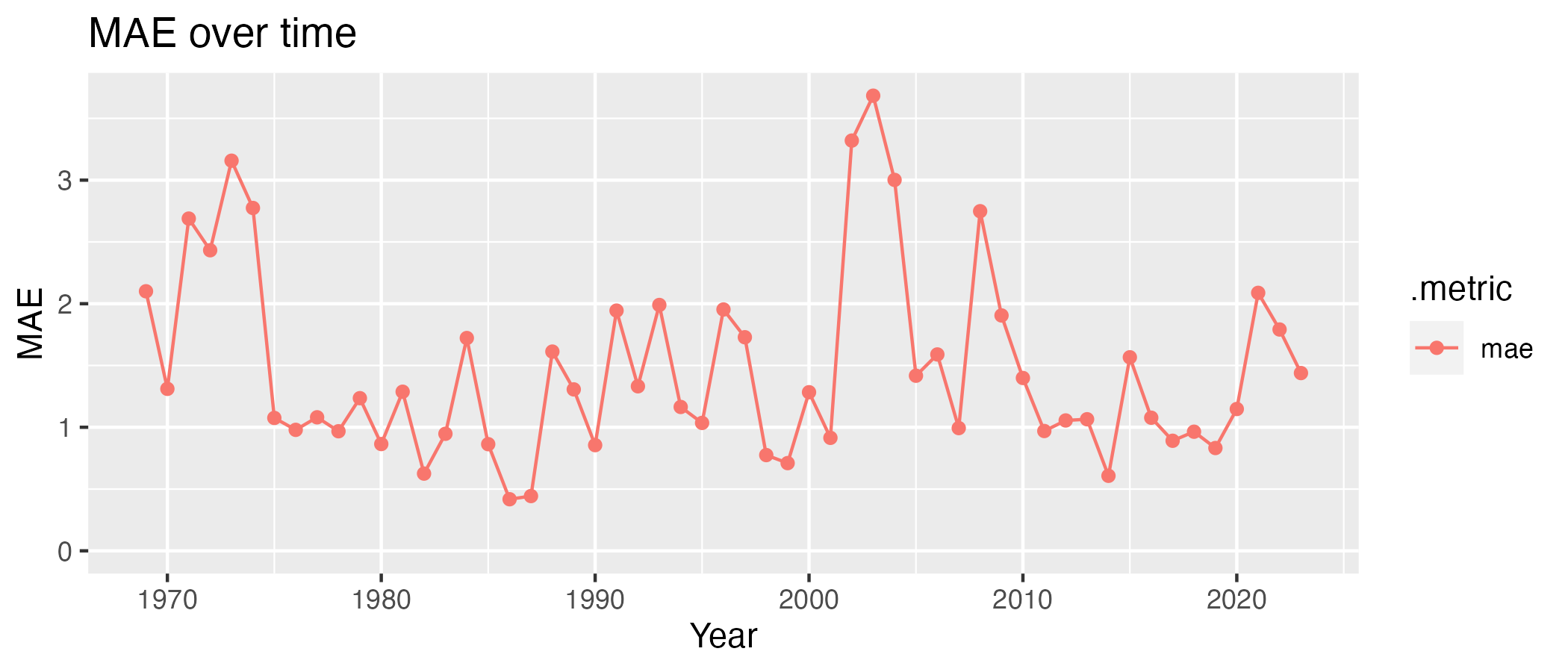
Interestingly, the worst predictions were for early 70s and around 2002-2004, not during the pandemic. This is indicative that the dynamics in Scotland changed around that time, and the model is not able to capture it as it was trained on data from a different country!
