✅ Week 09 Lab - Solutions
This solution file follows the format of the Quarto file .qmd you had to fill in during the lab session. If you want to render the document yourselves and play with the code, you can download the .qmd version of this solution file by clicking on the button below:
🥅 Learning Objectives
- Perform anomaly detection using various algorithms (k-means, DBSCAN, isolation forests, and LOF)
- Understand how different unsupervised learning algorithms can be used together to optimise anomaly detection
- Learn the basics of how to implement UMAP algorithm for dimensionality reduction.
⚙️ Setup
# Uncomment and run the lines below if needed (optional)
# install.packages("umap")
# install.packages("dbscan")
# install.packages("plotly")
# install.packages("isotree")
# install.packages("measurements")
# install.packages("scales")
# install.packages("devtools")
# To install vdemdata, uncomment the below line of code
# devtools::install_github("vdeminstitute/vdemdata")Load the libraries for today’s lab.
# Tidyverse packages we will use
library("tidymodels")
library("tidyverse")
# Non-tidymodels packages
library("dbscan")
library("ggsci")
library("isotree")
library("measurements")
library("NbClust")
library("plotly")
library("scales")
library("umap")
library("vdemdata")Part I - Meet a new dataset (5 mins)
In today’s lab, we will explore a pre-cleaned data set that contains the anonymised demographic profiles of OKCupid users. For those unaware, according to Wikipedia, OkCupid:
“… is a U.S.-based, internationally operating online dating, friendship, and formerly also a social networking website and application. It features multiple-choice questions to match members. Registration is free. OkCupid is owned by Match Group, which also owns Tinder, Hinge, Plenty of Fish, and many other popular dating apps and sites.”
df_okcupid <- read_csv("data/OK-cupid-demographic-data-cleaned.csv")
colnames(df_okcupid)The data set is quite large both in terms of rows (n = r comma(nrow(df_okcupid))) and columns (p = r ncol(df_okcupid)), so printing it (even as a tibble) will not necessarily be informative. Thankfully, however, the variable names are self-explanatory.
🗣CLASSROOM DISCUSSION (5 min)
(Your class teacher will mediate this discussion)
- How would you explore this data if dimensionality reduction was not an option?
Scatter plots for relationships between two continuous features. Box plots to assess relationships between continuous features over categorical features. As most features are categorical, however, frequency tables or heatmaps would be most useful.
- How would you answer: what are the most common types of profiles one can find on OK Cupid?
We could try k-means clustering and look at key quantities of interest such as the centroids of those clusters over a range of different features.
Part II - Dimensionality reduction with PCA (25 min)
🎯 ACTION POINTS
- To try to make sense of the sheer number of combinations of attributes, we will run PCA:
pca_recipe <-
recipe(~ ., data = df_okcupid) %>%
step_normalize(age, height) %>%
step_pca(all_predictors(), num_comp = 50, keep_original_cols=TRUE) %>%
prep()
# Apply the recipe to our data set
pca_results <- bake(pca_recipe, df_okcupid)- How much ‘information’ are we keeping after compressing the data with PCA?
If we take the first 5 principle components, we can explain over 50% of the variance among our features. This is quite remarkable given that our data set has r ncol(df_okcupid) columns.
pca_step <-
pca_recipe %>%
tidy() %>%
filter(type == "pca") %>%
pull(number)
pca_fit <- pca_recipe$steps[[pca_step]]$res
# the eigenvalues determine the amount of variance explained
eigenvalues <-
pca_fit %>%
tidy(matrix = "eigenvalues")
eigenvalues %>%
filter(PC <= 5) %>%
ggplot(aes(PC, cumulative)) +
geom_col(fill="#C63C4A") +
geom_text(aes(label=scales::percent(cumulative, accuracy=0.01)),
nudge_y=0.05, fontface="bold", size=rel(4.5)) +
# Customise scales
scale_y_continuous(name="Cumulative Explained Variance",
labels=scales::percent,
limits=c(0, 1),
breaks=seq(0, 1, 0.2)) +
scale_x_continuous(name="Principal Component") +
# Prettify plot a bit
theme_minimal() +
theme(panel.grid.minor = element_blank(),
panel.grid.major.x = element_blank(),
plot.title=element_text(size=rel(1.2)),
plot.subtitle = element_text(size=rel(1)),
axis.title=element_text(size=rel(1.3)),
axis.title.x=element_text(margin=margin(t=10)),
axis.title.y=element_text(margin=margin(r=10)),
axis.text=element_text(size=rel(1.2))) +
labs(title="The first PC explains ~33% of the variance in the data.\n Good compression!",
subtitle="The second PC adds some 7% more, and so on...",
caption="Figure 1. Explained variance\nper component") - Let’s focus on the first two components, as they are common plotting practices.
Think of the plot below as a ~37% compressed 2D representation of our 400+ numeric/dummy variables.
ggplot(pca_results, aes(PC01, PC02)) +
geom_point(alpha=0.2, size=rel(2.5)) +
scale_y_continuous(breaks=seq(-7.5, 7.5, 2.5), limits=c(-7.5, 7.5)) +
# Prettify plot a bit
theme_minimal() +
theme(panel.grid.minor = element_blank(),
plot.title=element_text(size=rel(1.2)),
plot.subtitle = element_text(size=rel(1)),
axis.title=element_text(size=rel(1.3)),
axis.title.x=element_text(margin=margin(t=10)),
axis.title.y=element_text(margin=margin(r=10)),
axis.text=element_text(size=rel(1.2))) +
labs(title = "There is a huge blob in the middle! I wonder what that represents.",
subtitle = "There are some clear outliers here",
caption = "Figure 2. Distribution of samples using\nPC01 and PC02 as coordinates.")- How concentrated is this main blob?
We can see that even when we set a low alpha=0.2(out of 1), there is no translucency in the main “blob”. This indicates a high density of observations.
Let’s change the geom() to see density instead of the dots:
ggplot(pca_results, aes(PC01, PC02)) +
geom_bin2d() +
scale_fill_viridis_b() +
# I tweaked those manually after seeing the plot
scale_y_continuous(breaks=seq(-7.5, 7.5, 2.5), limits=c(-7.5, 7.5)) +
# Prettify plot a bit
theme_minimal() +
theme(panel.grid.minor = element_blank(),
plot.title=element_text(size=rel(1.2)),
plot.subtitle = element_text(size=rel(1)),
axis.title=element_text(size=rel(1.3)),
axis.title.x=element_text(margin=margin(t=10)),
axis.title.y=element_text(margin=margin(r=10)),
axis.text=element_text(size=rel(1.2))) +
labs(title = "Here is how concentrated the main blob is",
subtitle = "It's time to put your understanding of plots to the test!",
caption = "Figure 3. Density of samples using\nPC01 and PC02 coordinates")🗣CLASSROOM DISCUSSION
(Your class teacher will mediate this discussion)
- How could you use the plots above to investigate the most common types of OK Cupid profiles?
We could use filtering to only include observations that lie within the yellow area of the graph. For example:
pca_results %>%
filter(between(PC01, 2.3, 2.8),
between(PC02, -1.5, 1.5))# A tibble: 4,523 × 519
age height ethnicity_asian offspring_doesnt_have_k…¹ speaks_english offspring_but_might_…² ethnicity_white
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 0.410 -0.808 0 0 0 0 1
2 -0.167 0.710 0 0 0 0 1
3 -0.263 0.710 0 0 1 0 1
4 0.0256 1.22 0 0 1 0 1
5 -0.551 0.204 0 0 1 0 1
6 0.122 1.22 0 1 0 1 1
7 0.795 -0.808 0 0 0 0 1
8 1.56 1.72 0 0 0 0 1
9 -1.03 0.457 0 1 1 0 1
10 2.62 1.22 0 0 1 0 1
# ℹ 4,513 more rows
# ℹ abbreviated names: ¹offspring_doesnt_have_kids, ²offspring_but_might_want_them
# ℹ 512 more variables: speaks_english_fluently <dbl>, speaks_spanish_poorly <dbl>, speaks_french_poorly <dbl>,
# speaks_french <dbl>, speaks_cpp <dbl>, offspring_doesnt_want_kids <dbl>, speaks_german_poorly <dbl>,
# ethnicity_black <dbl>, ethnicity_other <dbl>, speaks_chinese_okay <dbl>, speaks_spanish_okay <dbl>,
# offspring_but_wants_them <dbl>, speaks_sign_language_poorly <dbl>, ethnicity_hispanic_or_latin <dbl>,
# speaks_cpp_fluently <dbl>, speaks_spanish_fluently <dbl>, speaks_italian_okay <dbl>, …
# ℹ Use `print(n = ...)` to see more rows, and `colnames()` to see all variable namesWrite your answers and reflections here
🧑🏫 TEACHING MOMENT
Your class teacher will now guide the conversation and explain the plot below. If needed, they will recap how PCA works.
tidied_pca <- tidy(pca_recipe, pca_step)
plot_df <-
tidied_pca %>%
filter(component %in% paste0("PC", 1:5)) %>%
arrange(desc(abs(value))) %>%
group_by(component) %>%
# Get 10 biggest contributors to this PC
slice_head(n=10) %>%
mutate(component = fct_inorder(component))
terms_levels <-
plot_df %>%
group_by(terms) %>%
summarise(sum_value=sum(abs(value))) %>%
arrange(sum_value) %>%
pull(terms)
plot_df$terms <- factor(plot_df$terms, levels=terms_levels)
ggplot(plot_df, aes(value, terms, fill = abs(value))) +
geom_vline(xintercept = 0) +
geom_col() +
scale_fill_viridis_c(name="Abs value") +
facet_wrap(~component, nrow = 1) +
labs(title="Which variables contributed the most\n (together) to a particular PC?",
subtitle="This can be confusing. Make sure to ask your\n class teacher about any doubts you might have",
captions="Figure 4. Contribution of most important\n features to each component",
y = NULL) +
# Prettify plot a bit
theme_minimal() +
theme(plot.title=element_text(size=rel(1.2)),
plot.subtitle = element_text(size=rel(1)),
axis.title=element_text(size=rel(1.3)),
axis.title.x=element_text(margin=margin(t=10)),
axis.title.y=element_text(margin=margin(r=10)),
axis.text.y=element_text(size=rel(1.25)))🗣️ Discussion:
- How does Figure 4 help you interpret Figures 2 & 3?
We can see precisely which variables ended up contributing to each principle component. Therefore, higher PC02 values, for example, would be indicative of someone younger and taller than average.
- How does the above help you think about the attributes of the most common type of OKCupid profiles?
We can look at PC01 (the principle component that explains the largest variance among features), which shows that individuals who see star signs with moderate to low importance, speak English fluently, are male, white, single (perhaps obvious), drink socially, are straight and have fairly open diets tend to be the most prevalent OKCupid users.
- How would you interpret the 2D coordinates if instead of PC01 vs PC02, we had plotted PC01 vs PC03 in Figures 2 & 3?
Higher values on the y-axis would now indicate individuals who are both older and taller than average.
Part III: Anomaly detection techniques (45 mins)
👥 IN PAIRS, go through the action points below and discuss your impressions and key takeaways.
🎯 ACTION POINTS
- Take a look at the clusters identified by DBSCAN:
# Select the following hyperparameter values
eps = 1
minPts = 20
# Build the model
dbscan_fit <- dbscan::dbscan(pca_results[,c("PC01","PC02")], eps=eps, minPts = minPts)
# Add the cluster to pca_results and plot!
pca_results %>%
mutate(dbscan_cluster = factor(dbscan_fit$cluster)) %>%
ggplot(aes(PC01, PC02, color=dbscan_cluster, alpha=dbscan_cluster)) +
geom_point(size=rel(3.5)) +
scale_colour_manual(name="DBSCAN\nCluster", values=c(`0`="#C63C4A", `1`="#878787")) +
scale_alpha_manual(name="DBSCAN\nCluster", values=c(`0`=0.6, `1`=0.15)) +
scale_y_continuous(breaks=seq(-7.5, 7.5, 2.5), limits=c(-7.5, 7.5)) +
# Prettify plot a bit
theme_minimal() +
theme(panel.grid.minor = element_blank(),
plot.title=element_text(size=rel(1.5)),
plot.subtitle = element_text(size=rel(1.2)),
axis.title=element_text(size=rel(1.3)),
axis.title.x=element_text(margin=margin(t=10)),
axis.title.y=element_text(margin=margin(r=10)),
axis.text=element_text(size=rel(1.25))) +
labs(title="DBSCAN helps us identify outliers",
subtitle="The algorithm identified 2 different clusters, labelled 0 & 1",
captions="Figure 5. Clusters identified by DBSCAN")🗣 Discussion: How well do you think DBSCAN performs at anomaly detection on the two principle components?
It is pretty good, and we can visually perceive that. The algorithm is able to identify clear ‘outliers’ in the data. Just remember that we are looking at just the two principal components, and these two PCs don’t encode all the variables in the data the same way.
Based on the pre-selected values of the two hyperparameters, we can see that DBSCAN has identified 6 outliers that can be considered reasonable candidates. More experimentation may be needed, however, with these hyperparameters as we can see that a few values look like they could be outliers, and yet are not classified as such.
Admittedly, the pre-selected values we have used are somewhat arbitrary, and do not contain all points that could visually be considered as outliers (for example, the point on the far left of the graph). If we try lowering the epsilon neighbourhood to 0.5, to take one example, we can categorise 12 points as outliers.
Unfortunately, there is no hard and fast rule for selecting the best epsilon neighbourhood for a given data set. One way, however, is to calculate the distance between the nearest points for each value, setting the k-nearest neighbours equal to the minimum number of points. We then rank these values by distance and find the “knee” in the plot, which corresponds roughly to the optimal epsilon neighbourhood value. If you try this out, however, you will see that it is by no means fool-proof.
We adapted this code from here.
tibble(
dist = kNNdist(pca_results[,c("PC01","PC02")], k = minPts)
) %>%
arrange(dist) %>%
mutate(id = 1:n()) %>%
ggplot(aes(id, dist)) +
geom_hline(yintercept = 0.25, linetype = "dashed") +
geom_line() +
theme_minimal() +
theme(panel.grid.minor = element_blank(),
panel.grid.major.x = element_blank()) +
labs(x = "Points sorted by distance",
y = "20-NN distance",
title = "A neighbourhood of 0.25 is roughly optimal!")- Let’s filter to take a look at these samples:
(Ask your class teacher for help if you don’t know what we are doing here)
df_anomalies <-
pca_results %>%
mutate(
dbscan_cluster = as.factor(dbscan_fit$cluster),
outlier_type=case_when(
dbscan_cluster == 0 & PC02 > 2.5 ~ "upper side",
dbscan_cluster == 0 & PC02 < -2.5 ~ "lower side",
.default="Not an outlier"
)) %>%
filter(outlier_type != "Not an outlier") %>%
arrange(desc(outlier_type)) %>%
select(outlier_type, PC01, PC02, age, height, sex_m)
df_anomalies %>% knitr::kable()| outlier_type | PC01 | PC02 | age | height | sex_m |
|---|---|---|---|---|---|
| upper side | 2.134535 | 5.492575 | -0.4549691 | 6.529850 | 0 |
| upper side | 1.730021 | 6.131443 | -1.1277723 | 6.782886 | 1 |
| upper side | 3.082110 | 5.090541 | -0.4549691 | 5.770742 | 1 |
| lower side | 1.563825 | -4.635300 | -0.8394281 | -6.374985 | 1 |
| lower side | 1.084287 | -4.141511 | 2.2362436 | -3.844625 | 0 |
| lower side | 1.750879 | -4.853435 | -1.2238870 | -6.374985 | 0 |
The problem with the data frame above is that we are looking at the standardised values. It will probably be more helpful if we look at the original data instead.
💡 Do you see why we selected these particular variables here?
PC02 was mostly determined by age, height and, to a lesser extent, sex.
- Reverse the normalisation:
What were the mean and standard deviation of the normalized variables?
normalisation_step <- pca_recipe %>% tidy() %>% filter(type == "normalize") %>% pull(number)
normalisation_stats <- tidy(pca_recipe, normalisation_step)
normalisation_stats %>% knitr::kable()| terms | statistic | value | id |
|---|---|---|---|
| age | mean | 32.733604 | normalize_JOoyv |
| height | mean | 68.193986 | normalize_JOoyv |
| age | sd | 10.404231 | normalize_JOoyv |
| height | sd | 3.952007 | normalize_JOoyv |
Or in a more useful format:
normalisation_stats <- normalisation_stats %>%
pivot_wider(names_from="statistic", values_from="value")
normalisation_stats %>% knitr::kable()| terms | id | mean | sd |
|---|---|---|---|
| age | normalize_JOoyv | 32.73360 | 10.404231 |
| height | normalize_JOoyv | 68.19399 | 3.952007 |
Reverse-engineering the process for these variables:
age_stats <- filter(normalisation_stats, terms == "age")
height_stats <- filter(normalisation_stats, terms == "height")
df_anomalies %>%
mutate(age = age * age_stats$sd + age_stats$mean,
height = height * height_stats$sd + height_stats$mean,
# Convert from inches to meters
height = conv_unit(height, "inch", "m")) %>%
knitr::kable(col.names = c("outlier_type","PC01","PC02",'age','height (m)','sex_m'))| outlier_type | PC01 | PC02 | age | height (m) | sex_m |
|---|---|---|---|---|---|
| upper side | 2.134535 | 5.492575 | 28 | 2.3876 | 0 |
| upper side | 1.730021 | 6.131443 | 21 | 2.4130 | 1 |
| upper side | 3.082110 | 5.090541 | 28 | 2.3114 | 1 |
| lower side | 1.563825 | -4.635300 | 24 | 1.0922 | 1 |
| lower side | 1.084287 | -4.141511 | 56 | 1.3462 | 0 |
| lower side | 1.750879 | -4.853435 | 20 | 1.0922 | 0 |
💡 These are unusually tall and unusually short people on the upper and lower sides of the outliers, respectively.
- Small digression off-topic: Compare it to how k-means divides the data into k=2 clusters:
# Let's have a vote of the indices!
votes <-
NbClust(pca_results[,c("PC01","PC02")],
distance = "euclidean",
min.nc=2,
max.nc=8,
method = "kmeans",
index = "ch")
# This is how we can extract the "optimal" number of clusters
best_nclust <- votes$Best.nc[1]
# Run the model
kmeans_fit <- kmeans(pca_results[,c("PC01","PC02")], centers=best_nclust)
# Plot the results
pca_results %>%
mutate(cluster = as.factor(kmeans_fit$cluster)) %>%
ggplot(aes(PC01, PC02, color=cluster)) +
geom_point(size=rel(3.5), alpha=0.3) +
scale_y_continuous(breaks=seq(-7.5, 7.5, 2.5), limits=c(-7.5, 7.5)) +
theme_minimal() +
theme(panel.grid.minor = element_blank(),
plot.title=element_text(size=rel(1.5)),
plot.subtitle = element_text(size=rel(1.2)),
axis.title=element_text(size=rel(1.3)),
axis.title.x=element_text(margin=margin(t=10)),
axis.title.y=element_text(margin=margin(r=10)),
axis.text=element_text(size=rel(1.25))) +
scale_colour_bmj() +
labs(colour = "k-means\nCluster",
title="k-means captures a completely different pattern",
subtitle="What do you make of it?",
captions="Figure 6. Clusters identified by\nk-means with k=2 clusters")Clearly, k-means clustering does not make sense for anomaly detection. First of all, every observation belongs to a specific cluster with k-means. Furthermore, the algorithm arbitrarily divides the data into 5 more-or-less equal parts when unequal clustering into the “main blob” and outliers.
- Let’s try an isolation forest. The key hyperparameter of interest is the anomaly score, which we are going to vary.
Clearly, an isolation forest can be of great help to detect anomalies. In this case, setting a threshold of 0.75 resulted in 7 outliers, 6 of which correspond to the outliers found with dbscan. Furthermore, the observation at the far left of the graph has been classified as an outlier.
# We will test different values of the anomaly score
isoforests <-
crossing(th = seq(0.55, 0.8, by = 0.05),
nest(pca_results[,c("PC01","PC02")], .key = "data")) %>%
mutate(model = map(data, ~ isolation.forest(.x)),
score = map2(model, data, ~ predict(.x, newdata = .y, type = "score")),
outlier = map2(score, th, ~ .x > .y))
# Plot the results
isoforests %>%
select(th, data, outlier) %>%
unnest(c(data, outlier)) %>%
ggplot(aes(PC01, PC02, colour = outlier)) +
facet_wrap(. ~ paste("AS >", th)) +
geom_point(alpha = 0.25) +
theme_minimal() +
theme(panel.grid.minor = element_blank(),
legend.position = "bottom",
strip.text = element_text(hjust = 0, size = 10)) +
scale_colour_manual(values = ggsci::pal_aaas()(2)) +
labs(colour = "AS > Threshold")🗣 Discussion: What is the relationship between the anomaly score and the number of outliers in the data?
As the anomaly score increases, the number of outliers designated by the isolation forest will decrease.
- Let’s see if the Local Outlier Factor (LOF) performs better than DBSCAN/Isolation Forest.
We use the lof() function to calculate local outlier factors:
lof_results <- lof(pca_results[,c("PC01","PC02")], minPts = 5)
# Append the LOF score as a new column
pca_results$score <- lof_resultsWhat is the distribution of scores?
The distribution of scores is right-skewed, meaning there are many more observations at the left-hand side of the distribution, with the minority being classed as outliers.
pca_results %>%
ggplot(aes(x=score, fill=score >= 1.5)) +
geom_histogram(binwidth=0.025) +
scale_fill_manual(name="Comparatively\nHigh scores",
values=c(`FALSE`="#878787", `TRUE`="#C63C4A")) +
# Prettify plot a bit
theme_bw() +
theme(plot.title=element_text(size=rel(1.5)),
plot.subtitle = element_text(size=rel(1.2)),
axis.title=element_text(size=rel(1.3)),
axis.title.x=element_text(margin=margin(t=10)),
axis.title.y=element_text(margin=margin(r=10)),
axis.text=element_text(size=rel(1.25)),
legend.position = c(0.85, 0.3)) +
labs(title="The majority of samples have a score around 1.0",
subtitle="As we are looking for anomalies, our interest lies\n in the samples with outlier scores",
captions="Figure 7. Distribution of LOF scores")We can now plot the results of LOF.
pca_results %>%
ggplot(aes(PC01, PC02, size=score, alpha=score >= 1.5, color=score)) +
geom_point() +
scale_alpha_manual(name="LOF scores", values=c(`FALSE`=0.1, `TRUE`=0.6), guide="none") +
scale_radius(name="LOF scores", range=c(1, 10)) +
scale_color_viridis_c(name="LOF scores") +
# I tweaked those manually after seeing the plot
scale_y_continuous(breaks=seq(-7.5, 7.5, 2.5), limits=c(-7.5, 7.5)) +
# Prettify plot a bit
theme_bw() +
theme(plot.title=element_text(size=rel(1.2)),
plot.subtitle = element_text(size=rel(1)),
axis.title=element_text(size=rel(1.3)),
axis.title.x=element_text(margin=margin(t=10)),
axis.title.y=element_text(margin=margin(r=10)),
axis.text=element_text(size=rel(1.2))) +
labs(title = "Samples coloured and sized according to their LOF scores",
caption = "Figure 8. Samples coloured and sized\naccording to their LOF scores")🗣 Discussion: Does LOF perform better than DBSCAN or isolation forests to detect ‘anomalous’ samples?
This is maybe a bit of a trick question. Instead of thinking about anomalies in a global sense, the LOF looks at outliers by taking distinct areas of the graph and calculating outlier scores from that vantage point. DBSCAN and isolation forests (when properly tuned) by contrast look at global outliers.
LOF provides a different, complementary picture of the data. It doesn’t single out outliers but shows you how a particular sample is an outlier of its neighbourhood.
Part IV: Dimensionality reduction with UMAP (15 mins)
To round off our exploration of unsupervised learning with tabular data, we will look at UMAP (Uniform Manifold Approximation and Projection). UMAP, in essence, takes data that has a high number of dimensions and compresses it to a 2-dimensional feature space.
👉 NOTE: Andy Coenen and Adam Pearce of Google PAIR have put together an excellent tutorial on UMAP (click here).
vdem_subset <-
vdem %>%
as_tibble() %>%
filter(year >= 2010) %>%
transmute(country_year = paste(country_name, year, sep = "-"),
v2x_polyarchy, v2x_libdem, v2x_partipdem,
regime = case_when(v2x_regime == 0 ~ "Closed Autocracy",
v2x_regime == 1 ~ "Electoral Autocracy",
v2x_regime == 2 ~ "Electoral Democracy",
v2x_regime == 3 ~ "Liberal Democracy")) %>%
mutate(across(-c("regime","country_year"), ~ (.x-mean(.x))/sd(.x)))To explore this in the context of social science data, we will be looking at the Varieties of Democracy data set. Specifically, we will be looking at four different variables
v2x_polyarchy: Index of free and fair elections.v2x_libdem: Index of liberal democracy (protection of individuals / minorities from the tyranny of the state/majority).v2x_partip: Index of participatory democracy (participation of citizens in all political processes).v2x_regime: Four-fold typology of political regimes, namely, closed autocracy, electoral autocracy, electoral democracy, liberal democracy.
We will represent the three indices using a 3-d scatter plot, using colour to distinguish between regime type:
vdem_subset %>%
plot_ly(x = ~ v2x_polyarchy,
y = ~ v2x_libdem,
z = ~ v2x_partipdem,
color = ~ regime,
type = "scatter3d",
mode = "markers") %>%
layout(
scene = list(
xaxis = list(title = "Polyarchy"),
yaxis = list(title = "Liberal"),
zaxis = list(title = "Participation")
)
)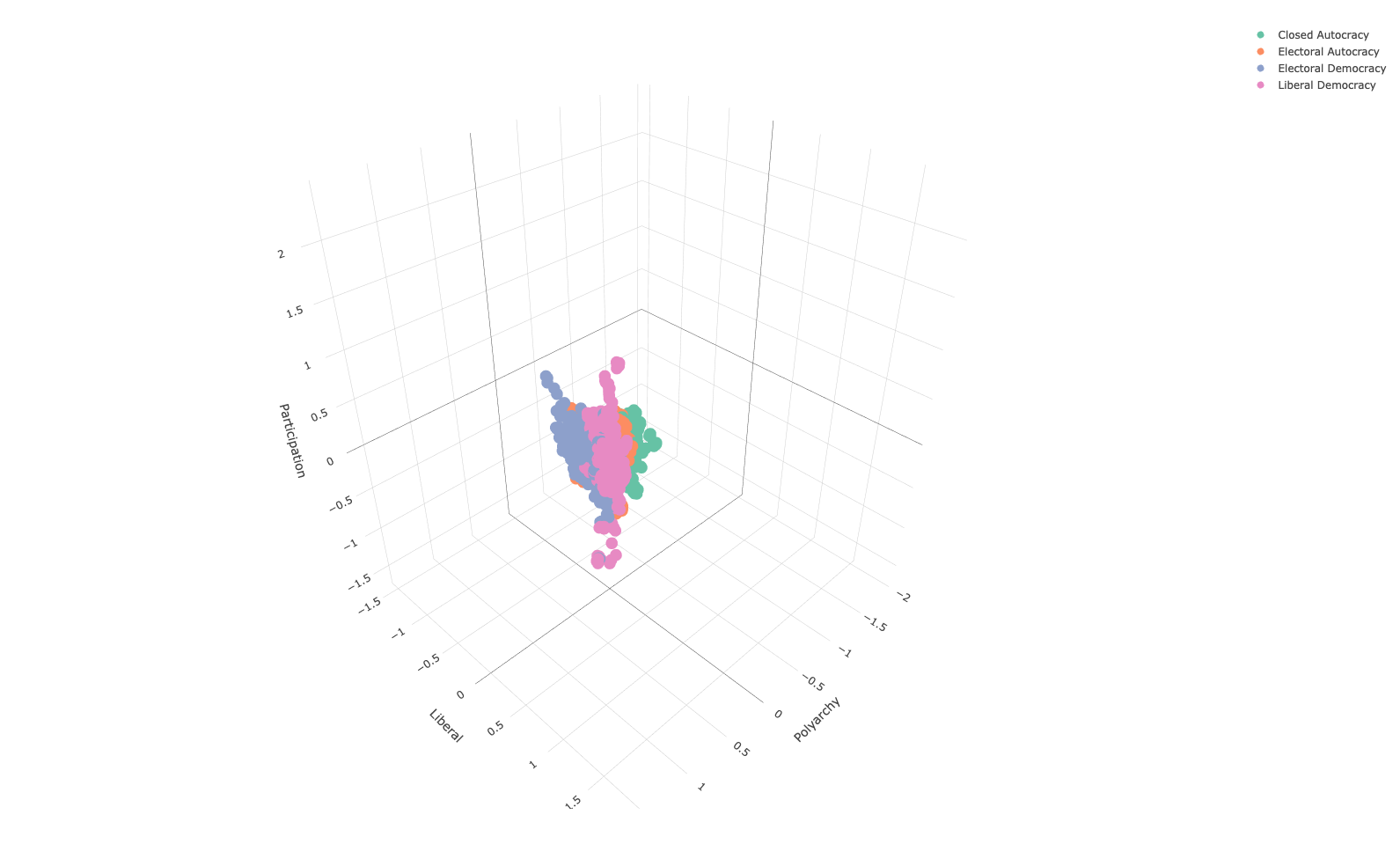
This is all good and well, but how can we represent this data as a 2-dimensional space? One increasingly popular method is UMAP. While we need to do some hand-waving as the mathematics are too complicated to be dealt with here, UMAP has a few key hyperparameters that can be experimented with.
- Number of nearest neighbours used to construct the initial high-dimensional graph (
n_neighbors). - Minimum distance between points in low dimensional space (
min_dist).
These hyperparameters (and more) can be explored by printing the following code:
umap.defaultsumap configuration parameters
n_neighbors: 15
n_components: 2
metric: euclidean
n_epochs: 200
input: data
init: spectral
min_dist: 0.1
set_op_mix_ratio: 1
local_connectivity: 1
bandwidth: 1
alpha: 1
gamma: 1
negative_sample_rate: 5
a: NA
b: NA
spread: 1
random_state: NA
transform_state: NA
knn: NA
knn_repeats: 1
verbose: FALSE
umap_learn_args: NAWe will change n_neighbors to 50, and use the three democracy indices to build a UMAP model.
custom.settings <- umap.defaults
custom.settings$n_neighbors <- 50
umap_vdem <- umap(vdem_subset[,2:4], custom.settings)After this, we can extract the 2-d space created by UMAP and plot it.
umap_vdem$layout %>%
as_tibble() %>%
ggplot(aes(V1, V2)) +
geom_point(alpha = 0.5, size = 2) +
theme_minimal() +
theme(panel.grid.minor = element_blank(),
legend.position = "bottom") +
labs(x = "Variable 1", y = "Variable 2", colour = NULL)To see how this pertains to value labels, we can add the regime classifications to this plot.
umap_vdem$layout %>%
as_tibble() %>%
mutate(regime = vdem_subset$regime) %>%
ggplot(aes(V1, V2, colour = regime)) +
geom_point(alpha = 0.5, size = 2) +
theme_minimal() +
theme(panel.grid.minor = element_blank(),
legend.position = "bottom") +
scale_colour_uchicago() +
labs(x = "Variable 1", y = "Variable 2", colour = NULL)Note: Just as you could use a step_pca to perform PCA, you can actually do the same for UMAP too! Have a look at step_umap from the embed library (see the documentation). You can have a look at how step_umap is applied on Julia Silge’s blog.
Note that UMAP has created a 2-map that maintains the topography of the data. Admittedly, this can be hard initially to interpret. However, we can note the following:
- This is a semi-circle configuration of points whereby less democratic regime types become more prominent as we travel from the top to the bottom.
- Despite this, we see considerable overlap between different regimes, indicating that considering these countries in at a given point in time to be distinctively democratic / autocratic may not be warranted in some cases.
- There is an outlier cluster that is distinct to the semi-circle configuration of points that UMAP provides. We can isolate these observations simply by filtering.
umap_vdem$layout %>%
as_tibble() %>%
bind_cols(vdem_subset, .) %>%
filter(V1>10) %>%
pull(country_year)[1] "Afghanistan-2022" "Afghanistan-2023" "North Korea-2010"
[4] "North Korea-2011" "North Korea-2012" "North Korea-2013"
[7] "North Korea-2014" "North Korea-2015" "North Korea-2016"
[10] "North Korea-2017" "North Korea-2018" "North Korea-2019"
[13] "North Korea-2020" "North Korea-2021" "North Korea-2022"
[16] "North Korea-2023" "Qatar-2010" "Qatar-2011"
[19] "Qatar-2012" "Qatar-2013" "Qatar-2014"
[22] "Qatar-2015" "Qatar-2016" "Qatar-2017"
[25] "Qatar-2018" "Qatar-2019" "Qatar-2020"
[28] "Qatar-2021" "Qatar-2022" "Qatar-2023"
[31] "China-2010" "China-2011" "China-2012"
[34] "China-2013" "China-2014" "China-2015"
[37] "China-2016" "China-2017" "China-2018"
[40] "China-2019" "China-2020" "China-2021"
[43] "China-2022" "China-2023" "Eritrea-2010"
[46] "Eritrea-2011" "Eritrea-2012" "Eritrea-2013"
[49] "Eritrea-2014" "Eritrea-2015" "Eritrea-2016"
[52] "Eritrea-2017" "Eritrea-2018" "Eritrea-2019"
[55] "Eritrea-2020" "Eritrea-2021" "Eritrea-2022"
[58] "Eritrea-2023" "Libya-2010" "Saudi Arabia-2010"
[61] "Saudi Arabia-2011" "Saudi Arabia-2012" "Saudi Arabia-2013"
[64] "Saudi Arabia-2014" "Saudi Arabia-2015" "Saudi Arabia-2016"
[67] "Saudi Arabia-2017" "Saudi Arabia-2018" "Saudi Arabia-2019"
[70] "Saudi Arabia-2020" "Saudi Arabia-2021" "Saudi Arabia-2022"
[73] "Saudi Arabia-2023" "United Arab Emirates-2010" "United Arab Emirates-2011"
[76] "United Arab Emirates-2012" "United Arab Emirates-2013" "United Arab Emirates-2014"
[79] "United Arab Emirates-2015" "United Arab Emirates-2016" "United Arab Emirates-2017"
[82] "United Arab Emirates-2018" "United Arab Emirates-2019" "United Arab Emirates-2020"
[85] "United Arab Emirates-2021" "United Arab Emirates-2022" "United Arab Emirates-2023"- This approach yields a very interesting finding: the most notoriously undemocratic regimes in the world such as Afghanistan under the Taliban, North Korea, and Eritrea all form a part of this cluster.
🏡 TAKE-HOME EXERCISE: How would you perform outlier detection on the OKCupid data with UMAP as a dimensionality reduction step instead of PCA?
