๐Ÿ Full code for life expectancy modelling (Week 5 lecture)

2023/24 Winter Term

Author

Dr. Ghita Berrada

Published

12 February 2024

The content below contains the full code that was used to do the exploratory data analysis and linear regression modelling from the case study from the Week 05 lecture. The case study explored the WHO Life expectancy dataset from Kaggle, which is a dataset that aims at studying which factors affect life expectancy.

Click on the button below to download the source files (.csv dataset and .ipynb notebook) that were used to create this page, if you ever want to try the code for yourselves:

(this is a zip file because there are source code files in it)

Python library imports

As usual, before starting our analysis/modelling, we import the Python libraries we need to do the job (this week, in addition to the usual libraries, you might need to install the missingno library, the sklearn library, the statsmodels library and the miceforest library1).

import missingno as msno #missing data analysis library
import pandas as pd 
import numpy as np
import math

#Data visualization
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
colors = ['#c1121f','#669bbc', '#f4d35e', '#e9724c', '#ffc857']
plt.style.use('seaborn-v0_8-white')
plt.rc('figure', figsize=(12,8))
plt.rc('font', size=18)
plt.rc('axes', labelsize=14, titlesize=14)
plt.rc('legend', fontsize=14)
plt.rc('xtick', labelsize=10)
plt.rc('ytick', labelsize=10)

#Preprocessing and modelling
from sklearn.impute import KNNImputer #import for KNN imputation
from sklearn.impute import SimpleImputer #import for mean/median imputation
import miceforest as mf # import for multiple imputation
import statsmodels.api as sm
from statsmodels.tools.eval_measures import rmse
from scipy.stats import skew, kurtosis

#General
import warnings 
warnings.filterwarnings(action='ignore') # ignoring warning messages from packages
import re #library to use regular expressions (useful in data cleaning e.g columns renaming)

Reading the dataset file

We read the .csv file that contains our dataset into a Pandas dataframe that we can manipulate.

data = pd.read_csv("Life_Expectancy_Data.csv")

Checking the properties of the dataset columns

We check the properties of the columns/variables of our dataset.

data.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 2938 entries, 0 to 2937
Data columns (total 22 columns):
 #   Column                           Non-Null Count  Dtype  
---  ------                           --------------  -----  
 0   Country                          2938 non-null   object 
 1   Year                             2938 non-null   int64  
 2   Status                           2938 non-null   object 
 3   Life expectancy                  2928 non-null   float64
 4   Adult Mortality                  2928 non-null   float64
 5   infant deaths                    2938 non-null   int64  
 6   Alcohol                          2744 non-null   float64
 7   percentage expenditure           2938 non-null   float64
 8   Hepatitis B                      2385 non-null   float64
 9   Measles                          2938 non-null   int64  
 10   BMI                             2904 non-null   float64
 11  under-five deaths                2938 non-null   int64  
 12  Polio                            2919 non-null   float64
 13  Total expenditure                2712 non-null   float64
 14  Diphtheria                       2919 non-null   float64
 15   HIV/AIDS                        2938 non-null   float64
 16  GDP                              2490 non-null   float64
 17  Population                       2286 non-null   float64
 18   thinness  1-19 years            2904 non-null   float64
 19   thinness 5-9 years              2904 non-null   float64
 20  Income composition of resources  2771 non-null   float64
 21  Schooling                        2775 non-null   float64
dtypes: float64(16), int64(4), object(2)
memory usage: 505.1+ KB

Data cleaning: renaming of column names

Before we proceed with the analysis, we do some data cleaning i.e we rename mis-named columns (e.g the variable originally named thinness 1-19 years instead of thinness 10-19 years), rename columns to remove trailing and leading spaces from column names as any special characters (e.g spaces, โ€œ-โ€, โ€œ/โ€) and make the column names lowercase.

columns_names = []
for column in data.columns:
    if column == ' thinness  1-19 years':  #the variable that was originally misnamed as thinness  1-19 years is renamed (while dealing with special characters) thinness_10_19_years
        column = 'thinness_10_19_years'
    else:
        column = re.sub("\s|-|/","_",column.strip(' ').replace("  ", " ")) #removing leading/trailing spaces in column names and dealing with special characters
        column = column.lower() #making column names lowercase
        
    columns_names.append(column)

data.columns = columns_names
data.head() # checking processing of column names by printing first rows of dataframe
country year status life_expectancy adult_mortality infant_deaths alcohol percentage_expenditure hepatitis_b measles ... polio total_expenditure diphtheria hiv_aids gdp population thinness_10_19_years thinness_5_9_years income_composition_of_resources schooling
0 Afghanistan 2015 Developing 65.0 263.0 62 0.01 71.279624 65.0 1154 ... 6.0 8.16 65.0 0.1 584.259210 33736494.0 17.2 17.3 0.479 10.1
1 Afghanistan 2014 Developing 59.9 271.0 64 0.01 73.523582 62.0 492 ... 58.0 8.18 62.0 0.1 612.696514 327582.0 17.5 17.5 0.476 10.0
2 Afghanistan 2013 Developing 59.9 268.0 66 0.01 73.219243 64.0 430 ... 62.0 8.13 64.0 0.1 631.744976 31731688.0 17.7 17.7 0.470 9.9
3 Afghanistan 2012 Developing 59.5 272.0 69 0.01 78.184215 67.0 2787 ... 67.0 8.52 67.0 0.1 669.959000 3696958.0 17.9 18.0 0.463 9.8
4 Afghanistan 2011 Developing 59.2 275.0 71 0.01 7.097109 68.0 3013 ... 68.0 7.87 68.0 0.1 63.537231 2978599.0 18.2 18.2 0.454 9.5

5 rows ร— 22 columns

Dataset nullity matrix

We produce the nullity matrix corresponding to our dataset to get a better picture of the missingness patterns within our dataset. There seems to be a MAR mechanism at play hereโ€ฆWe save the matrix as figure.

```{python}
ax=msno.matrix(data)
fig_copy = ax.get_figure()
fig_copy.savefig("who_missingness_matrix.png",bbox_inches = 'tight')
```

Producing density plots for life expectancy per country status

We use the seaborn library to produce density plots of life expectancy per country status (i.e developed vs developing countries). This allows us to see that life expectancy seems to follow two distinct distributions depending on whether the countries are classified as developed or developing. If we were to really model things properly (and not over-simplistically as we are doing now), we might need distinct models for life expectancy per country status.

data_developed = data.loc[data['status']=='Developed'].copy() #selecting the data that corresponds to developed countries
data_developing = data.loc[data['status']=='Developing'].copy() # selecting the data that corresponds to developing countries
```{python}
sns.kdeplot(data_developed['life_expectancy'],  # Plot the density of life expectancy for developed countries
            label='Developed',  # Label the developed countries' density plot
            fill=True,  # Fill the area under the density curve
            color = colors[0],  # Set the color of the developed countries' density plot
            alpha = 0.8)  # Set the transparency of the developed countries' density plot

sns.kdeplot(data_developing['life_expectancy'],  # Plot the density of life expectancy for developing countries
            label='Developing',  # Label the developing countries' density plot
            fill=True,  # Fill the area under the density curve
            color=colors[1],  # Set the color of the developing countries' density plot
            alpha = 0.8)  # Set the transparency of the developing countries' density plot

plt.legend(loc='upper left')  # Add a legend to the plot
plt.ylabel('Density')  # Label the y-axis as "Density"
plt.xlim(30,95)  # Set the limits of the x-axis
plt.xlabel('Life Expectancy (years)')  # Label the x-axis as "Life Expectancy (years)"
plt.title('Life Expectancy based on Status \n', fontsize=18);  # Set the title of the plot
plt.savefig("life_expectancy_kde.png")
```

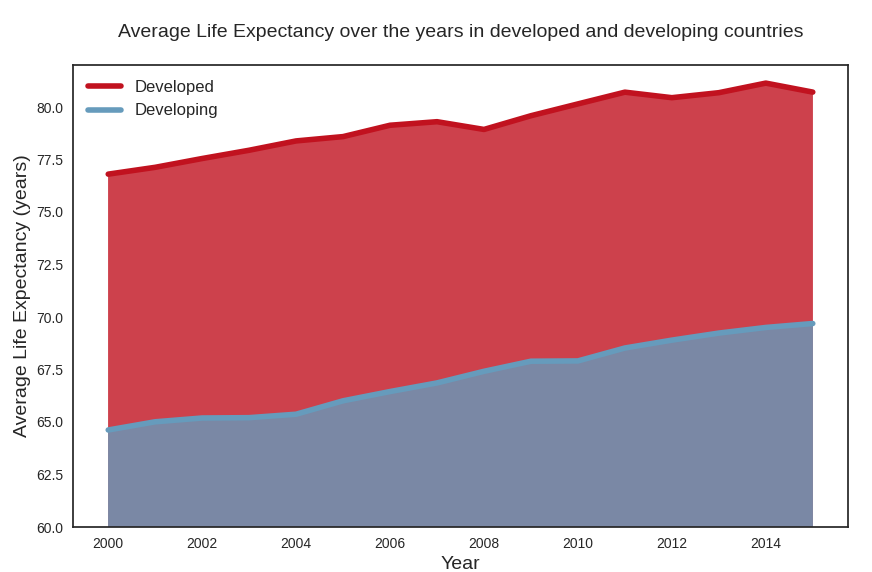
Average life expectancy plot

We plot the average of life expectancy over the years, differentiating between developed and developing countries. This is again a plot that confirms that life expectancy in developed countries follows a distinct pattern from life expectancy in developing countries.

```{python}
# Plot average Life Expectancy over the years
fig, ax = plt.subplots(figsize=(10,6))

ax.plot(data_developed.groupby('year')['life_expectancy'].mean(),
       label='Developed',
       color=colors[0],
       linewidth=4)

# Fill area between the line plot and the x-axis
ax.fill_between(data_developed.groupby('year')['life_expectancy'].mean().index,
                data_developed.groupby('year')['life_expectancy'].mean().values,
                color=colors[0],
                alpha=0.8) 

ax.plot(data_developing.groupby('year')['life_expectancy'].mean(),
       label='Developing',
       color=colors[1],
       linewidth=4,)

ax.fill_between(data_developing.groupby('year')['life_expectancy'].mean().index,
                data_developing.groupby('year')['life_expectancy'].mean().values,
                color=colors[1],
                alpha=0.8) 

plt.legend(loc='upper left', fontsize=12)
ax.set_xlabel('Year')
ax.set_ylabel('Average Life Expectancy (years)')

# Set y-axis limits
ax.set_ylim(60,82)

ax.set_title('Average Life Expectancy over the years in developed and developing countries\n');
plt.savefig("avg_life_expectancy_peryear.png")
```

Dataset variables correlation heatmap

We draw the correlation heatmap between the variables in our dataset (the heatmap represents the Pearson correlation coefficient between variables i.e only captures linear relationships between variables). In red, are highly positively correlated variables and blue highly negatively correlated variables.

From the correlation heatmap, we can conclude the following:

  • the dependent variable i.e life expectancy has a high positive correlation with the features schooling, income_composition_of_resources, and bmi, and a high negative correlation with the features adult_mortality and hiv_aids.
  • the features schooling and income_composition_of_resources also have a high correlation between them, as do adult_mortality and hiv_aids.
  • though some features do not have to a high correlation with the dependent variable, it is still important to visualize the relationship between these features and life expectancy graphically. This is because the heatmap only captures linear relationships between variables (since it shows the Pearson coefficient) and does not capture other types of relationships that the dependent variable may have with the other variable, which may well be relevant and important (though our focus in this lecture was exclusively linear relationships).
```{python}
plt.figure(figsize=(17,17))

heatmap_colors = [colors[1], '#d6d5c9', colors[0]]

corr = data.corr()
mask = np.triu(np.ones_like(corr, dtype=bool))

sns.heatmap(data.corr(), 
            mask=mask,
            center=0,
            annot=True,
            fmt='.2f',
            cmap=heatmap_colors,
            square=True,
            linewidths=.2,
            cbar_kws={"shrink": .6})

plt.title('Features Correlation Matrix Heatmap', fontsize=25);
plt.savefig("who_correlation_heatmap.png",bbox="tight")
```

Plotting scatterplots of variables relationships

Next, weโ€™ll plot a series of scatterplots to graphically evaluate the relationships between life_expectancy and the other variables. First, we start by defining a function that plots scatterplots of life_expectancy (in the y-axis) versus other variables (in the x-axis) and colors each of the data points depending on whether the data point belongs to a developed or developing country.

```{python}
#Function to plot scatter plots
def plot_scatterplot(df, features, title = 'Features', columns = 2, x_lim=None):
    
    df = df.copy()
    
    rows = math.ceil(len(features)/2)

    fig, ax = plt.subplots(rows, columns, sharey = True, figsize = (14,14))
    
    for i, feature in enumerate(features):
        ax = plt.subplot(rows, columns, i+1)
        sns.scatterplot(data = df,
                        x = feature,
                        y = 'life_expectancy',
                        hue = 'status',
                        palette=[colors[1], colors[0]],
                        ax = ax)
        if (i == 0):
            ax.legend()
        else:
            ax.legend("")
        
    fig.legend(*ax.get_legend_handles_labels(), 
               loc='lower center', 
               bbox_to_anchor=(1.04, 0.5),
               fontsize='small')
    fig.suptitle('{} x Life Expectancy'.format(title), 
                 fontsize = 25, 
                 x = 0.56);

    fig.tight_layout(rect=[0.05, 0.03, 1, 1])
```

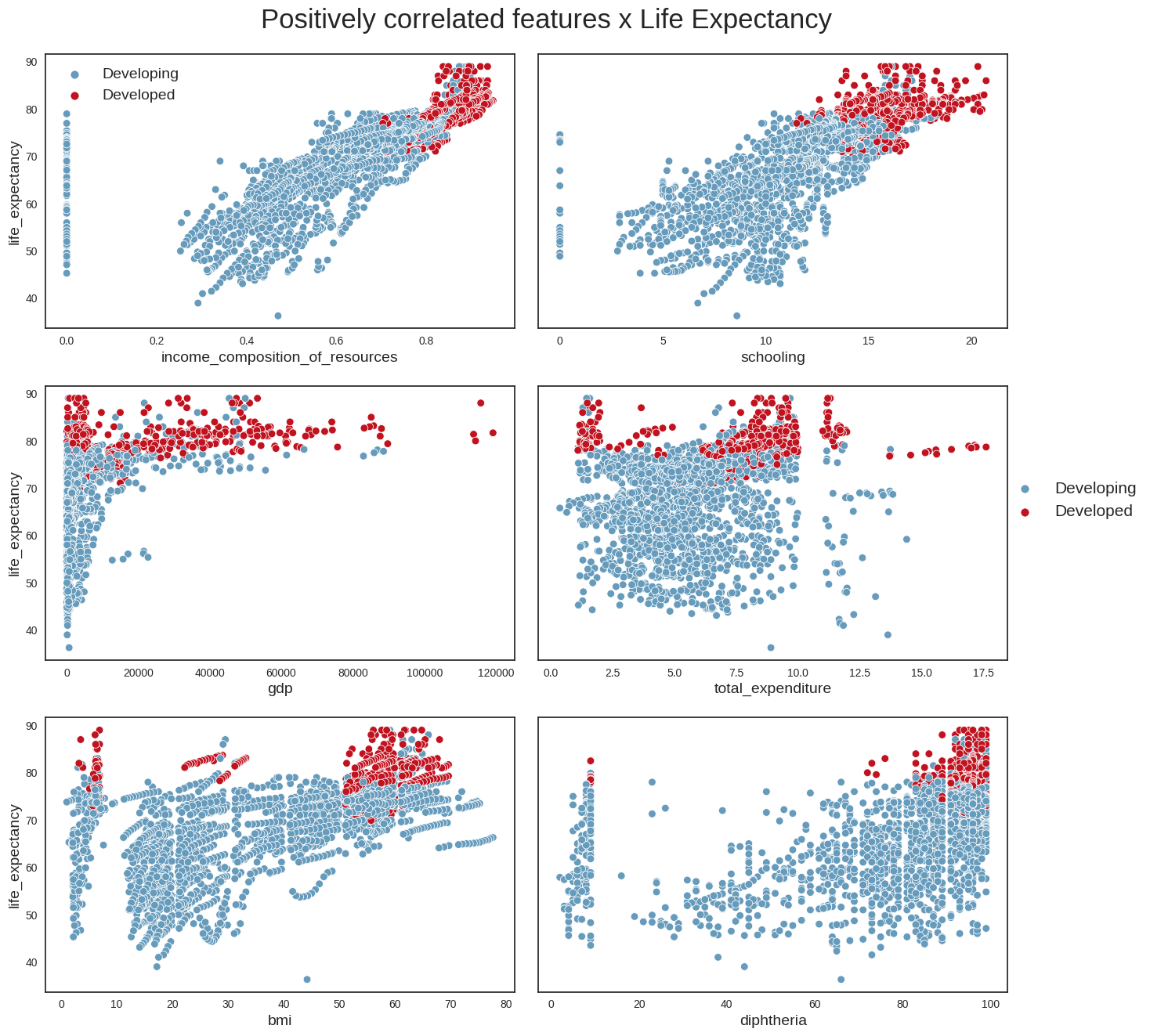
We use this function to first draw scatterplots of life_expectancy versus positively correlated variables (i.e income_composition_of_resources,schooling,gdp,total_expenditure,bmi and diphtheria).

```{python}
#Plot Life Expectancy x positively correlated features
pos_correlated_features = ['income_composition_of_resources', 'schooling', 
                           'gdp', 'total_expenditure', 
                           'bmi', 'diphtheria']

title = 'Positively correlated features'

plot_scatterplot(data, pos_correlated_features, title)
plt.savefig("pos_corr_variables.png", bbox_inches='tight')
```

Then, we draw the scatterplots of life_expectancy versus negatively correlated variables (i.e adult_mortality,hiv_aids,thinness_10_19_years,infant_deaths)

```{python}
#Plot Life Expectancy x negatively correlated features
neg_correlated_features = ['adult_mortality', 'hiv_aids', 
                           'thinness_10_19_years', 'infant_deaths']

title = 'Negatively correlated features'

plot_scatterplot(data, neg_correlated_features, title)

plt.savefig('neg_corr_variables.png', bbox_inches='tight')
```

And, finally, we draw the scatterplots of life_expectancy versus some additional variables such as population and alcohol.

```{python}
#Check other correlations
data_temp = data.loc[data['population'] <= 1*1e7, :] 
features = ['population', 'alcohol']
plot_scatterplot(data_temp, features)
plt.savefig("other_corr.png",bbox_inches='tight')
```

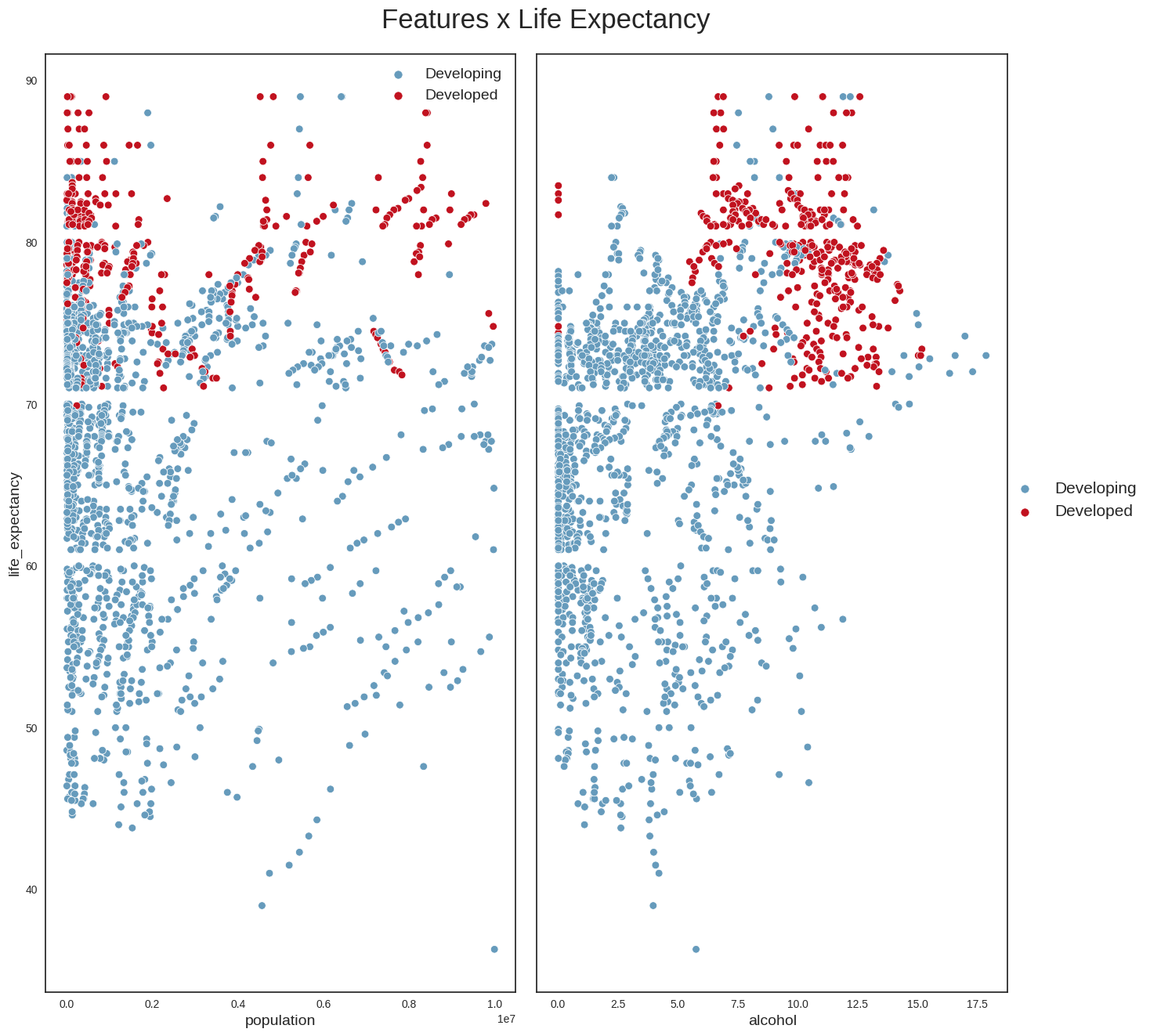
From these plots, we can conclude the following: - we can confirm that life_expectancy does indeed have strong linear relationships with some variables (e.g income_compostion_of_resources,schooling,adult_mortality) - it looks as if the absolute number of a countryโ€™s population does not have a direct relationship with life expectancy; a more interesting variable perhaps might have been population density, which could provide more clues about the countryโ€™s social and geographical conditions - Another interesting point is that countries with the highest alcohol consumption also seem to have the highest life expectancies. This looks however to be the classic case for using the maxim โ€˜Correlation does not imply causationโ€™. The life expectancy of someone who owns a Ferrari is possibly higher than that of the rest of the population, but that does not mean that buying a Ferrari will increase their life expectancy. The same applies to alcohol. One hypothesis is that in developed countries, the populationโ€™s average has better financial conditions, allowing for greater consumption of luxury goods such as alcohol. We probably see a similar phenomenon with BMI: countries with the highest average BMI have the highest life expectancies, which looks counterintuitive, and is probably more aa reflection of these countriesโ€™ financial condition and level of development.

Independent variables distributions

We next examine the distributions of the independent variables (the goal here is to check for the existence of outliers in each of the independent variables).

```{python}
#Function to plot distribution 
def plot_distribution(df, columns, title="Distribution of Features"):
    
    df = df.copy()
    
    rows = math.ceil(len(columns)/2)
    
    fig, ax = plt.subplots(rows, 2, figsize = (14,14))
    
    for i, column in enumerate(columns):
        ax = plt.subplot(rows, 2, i+1)

        sns.kdeplot(data.loc[data['status']=='Developed', column], 
                    label='Developed',
                    fill=True, 
                    color = colors[0],
                    alpha = 0.8, 
                    ax = ax)

        sns.kdeplot(data.loc[data['status']=='Developing',column], 
                    label = 'Developing',
                    fill = True,
                    color = colors[1],
                    alpha = 0.8,
                    ax = ax)
    
        ax.set_xlabel(column)
        ax.set_ylabel('')
    
    fig.legend(labels=['Developed', 'Developing'], 
               loc='center right', 
               bbox_to_anchor=(1.145, 0.5))
    
    fig.suptitle(title, 
                 fontsize=24,
                 x = 0.56);
    
    fig.text(0.04, 0.5, 
             'Density', 
             va='center', 
             rotation='vertical', 
             fontsize=16)
    
    fig.tight_layout(rect=[0.05, 0.03, 1, 1])
```

We plot the distribution of the positively correlated variables:

```{python}
title = 'Distribution of Positively correlated features'
plot_distribution(data, pos_correlated_features, title)
plt.savefig("dist_pos_corr_features.png",bbox_inches="tight")
```

And the distribution of the negatively correlated variables:

```{python}
title = 'Distribution of Negatively correlated features'
plot_distribution(data, neg_correlated_features, title)
plt.savefig("dist_neg_corr_features.png",bbox_inches="tight")
```

As well as the distribution of other variables such as population and alcohol:

```{python}
plot_distribution(data_temp, features)
plt.savefig("dist_other_features.png",bbox_inches="tight")
```

```{python}
#Function to plot box plot
def plot_boxplot(df, columns, title = 'Box plot of features'):
      
    df = df.copy()
    
    rows = math.ceil(len(columns)/2)
    
    fig, ax = plt.subplots(rows, 2, figsize = (14,14))
    
    for i, column in enumerate(columns):
        ax = plt.subplot(rows, 2, i+1)
        
        sns.boxplot(x = df[column], 
                    data = df, 
                    ax = ax, 
                    color = colors[0])
    
        ax.set_xlabel(column)
        ax.set_ylabel('')
    
    fig.suptitle(title, 
                 fontsize=24,
                 x = 0.56);
    
    fig.text(0.04, 0.5, 
             'Density', 
             va='center', 
             rotation='vertical', 
             fontsize=16)
    
    fig.tight_layout(rect=[0.05, 0.03, 1, 1])  
```

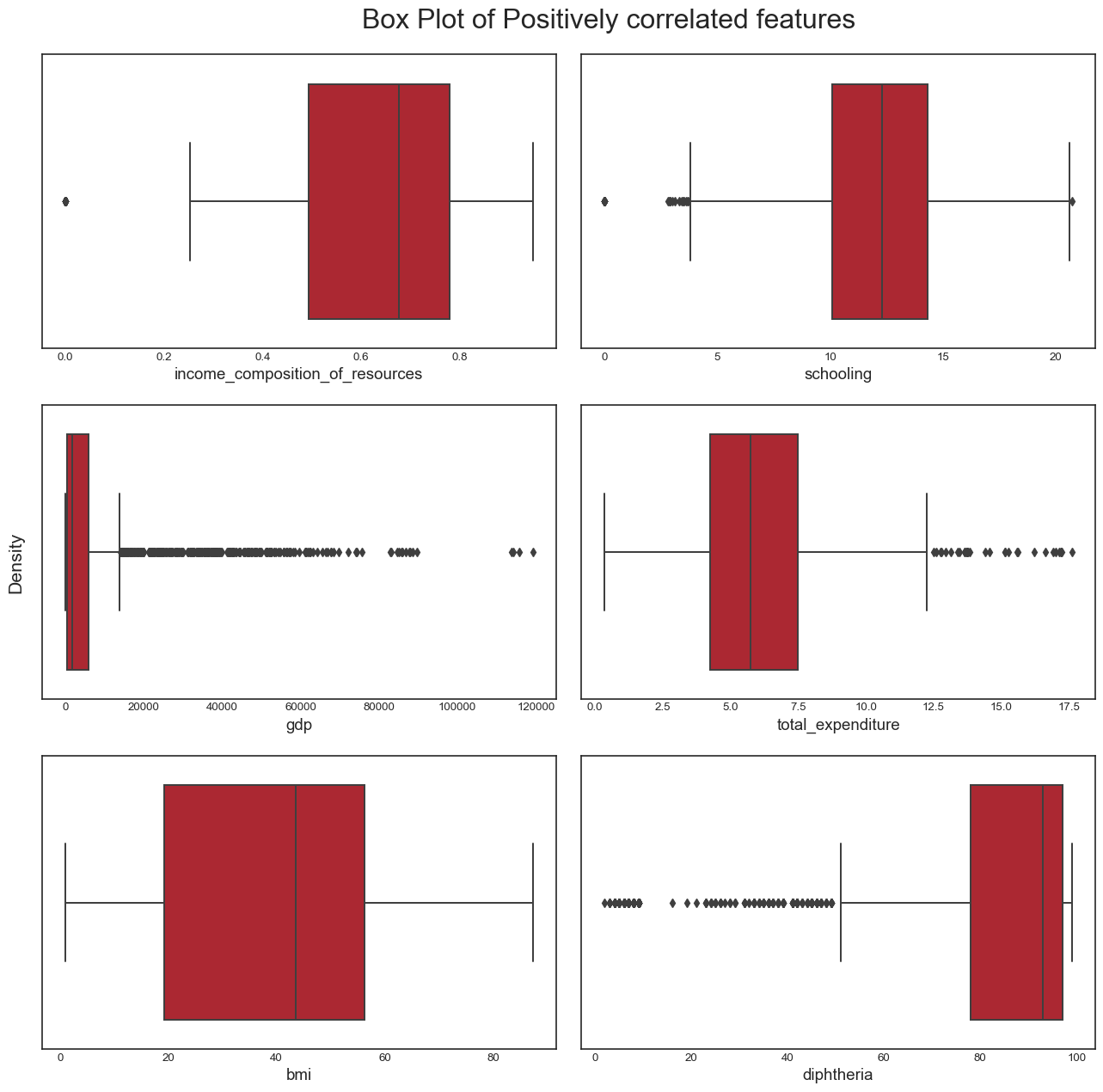
We draw the boxplots for the positively correlated variables:

```{python}
title = 'Box Plot of Positively correlated features'
plot_boxplot(data, pos_correlated_features, title)
plt.savefig('boxplot_pos_corr_features.png',bbox_inches="tight")
```

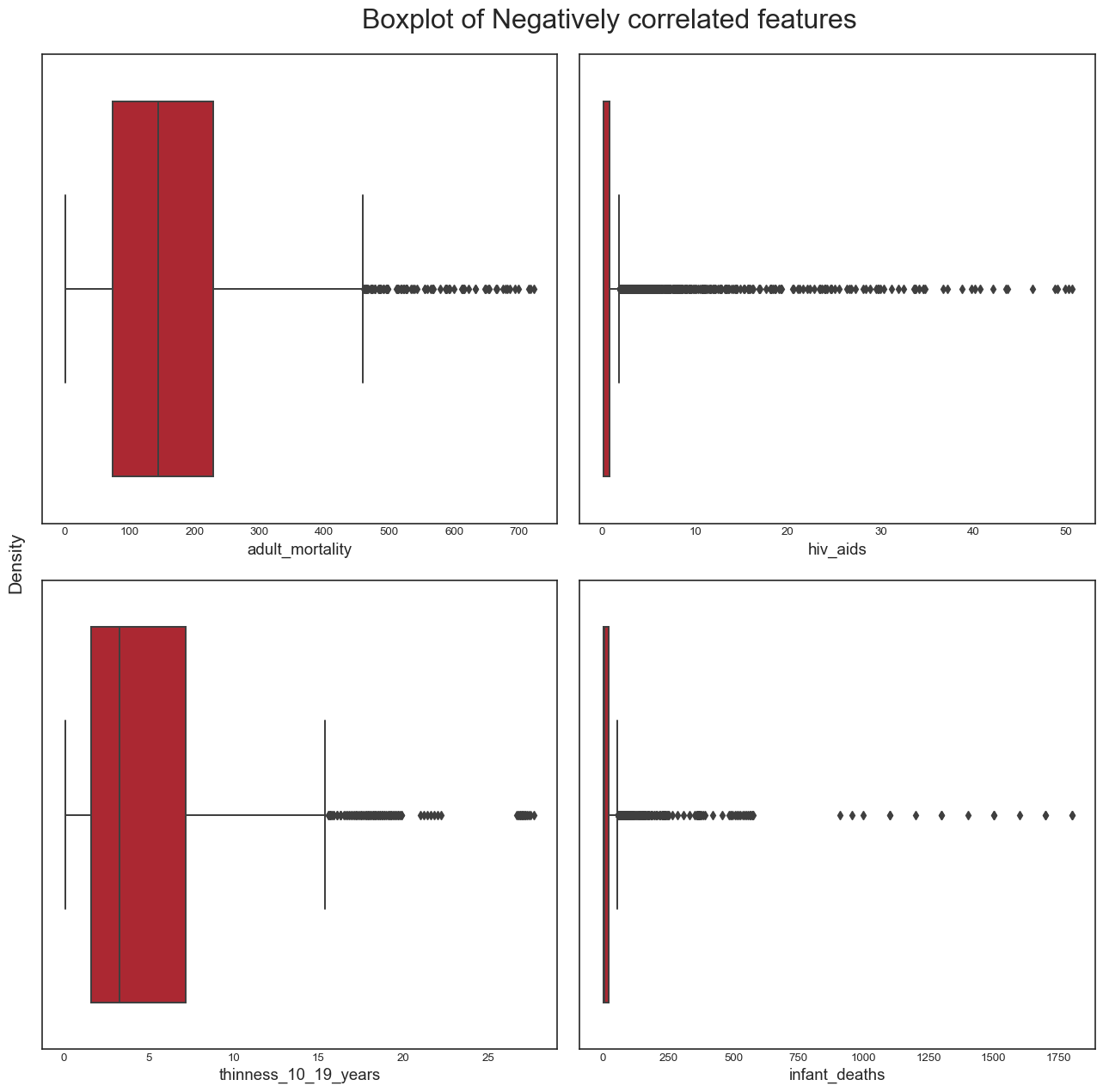
And the boxplots for negatively correlated variables:

```{python}
title = 'Boxplot of Negatively correlated features'
plot_boxplot(data, neg_correlated_features, title)
plt.savefig('boxplot_neg_corr_features.png',bbox_inches="tight")
```

And finally, the boxplots for variables such as population and alcohol:

```{python}
plot_boxplot(data_temp, features, "Boxplot of other features")
plt.savefig("boxplot_other_features.png",bbox_inches="tight")
```

From this analysis, we conclude the following: - the dataset seems to have a significant amount of outliers that would need to be treated. It is highly likely that some of these outliers are actually valid data: some countries may have metrics that are very different from the others e.g China and India have a population almost 5 times larger than the third most populous country in the world, the USA. However, it is also plausible to assert that many of the outliers are likely to be errors introduced during data computation or entry. Some ways to deal with outliers might be to remove them (not desirable as it would result in huge loss of data) or removing the outliers, treating them as missing data and doing data imputation (the idea here is to replace the outlier data by data that comes from the same distribution as the rest of the dataset). - again, we confirmed this trend of developing countries and developed countries of having distinct variable distributions

Removing the country column, making status numerical and imputing missing values

Next, we do a bit of data cleaning: - we remove the country column (itโ€™s irrelevant in our analysis) - we make the status column numerical (we substitute the value of 1 for โ€˜Developedโ€™ and 0 for โ€˜Developingโ€™) - we fill in missing values in the data by imputation

data_num = data.drop(columns='country', axis=1, inplace=False) #dropping the `country` column - Note that we produce a copy of the original dataframe here and keep the original dataframe intact
data_num['status'].replace(['Developing', 'Developed'], [0, 1], inplace=True) #we replace the values of status i.e "Developing" and "Developed" by 0 and 1 respectively
d=data_num.isnull().sum() #checking the number of missing values per variable in the dataframe
d
year                                 0
status                               0
life_expectancy                     10
adult_mortality                     10
infant_deaths                        0
alcohol                            194
percentage_expenditure               0
hepatitis_b                        553
measles                              0
bmi                                 34
under_five_deaths                    0
polio                               19
total_expenditure                  226
diphtheria                          19
hiv_aids                             0
gdp                                448
population                         652
thinness_10_19_years                34
thinness_5_9_years                  34
income_composition_of_resources    167
schooling                          163
dtype: int64

We get the list of features that have null values (i.e missing values):

null_features = d.where(d>0).dropna().index.tolist()

We impute missing values using four different methods (i.e mean imputation, median imputation, KNN imputation, multiple imputation):

#KNN imputation
imp_knn = KNNImputer()
imputed_knn = imp_knn.fit_transform(data_num)
data_imp_knn = pd.DataFrame(imputed_knn, columns=data_num.columns) #complete dataset for KNN imputation

#mean imputation
imp_mean = SimpleImputer(strategy='mean')
imputed_mean = imp_mean.fit_transform(data_num)
data_imp_mean = pd.DataFrame(imputed_mean, columns=data_num.columns) #complete dataset for mean imputation

#median imputation
imp_median = SimpleImputer(strategy='median')
imputed_median = imp_median.fit_transform(data_num)
data_imp_median = pd.DataFrame(imputed_median, columns=data_num.columns) #complete dataset for median imputation

#multiple imputation or MICE
kds = mf.ImputationKernel(
  data_num,
  save_all_iterations=True,
  random_state=100
)
# Run the MICE algorithm for 10 iterations
kds.mice(10)
# Return the completed dataset (for MICE)
data_imp_mice = kds.complete_data()

And we confirm that our datasets, after imputation, no longer contain missing values:

print(data_imp_mice.isnull().values.any(), data_imp_knn.isnull().values.any(),
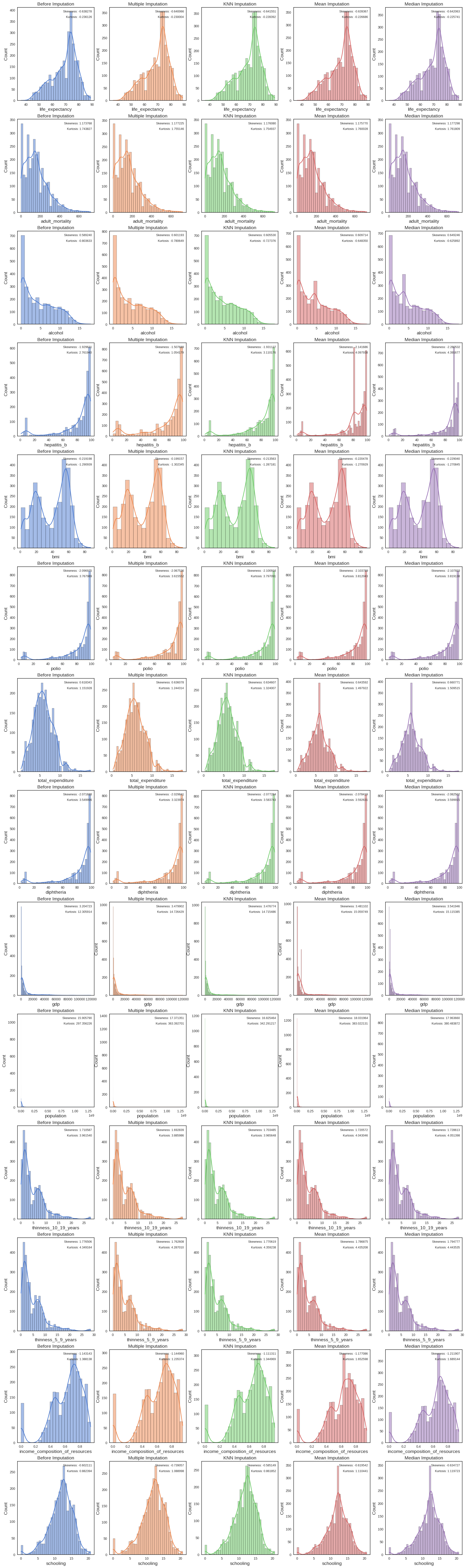
      data_imp_mean.isnull().values.any(), data_imp_median.isnull().values.any())
False False False False

We next draw the distributions of our data before and after imputation and compare skewness and kurtosis for each of the variables

Code to plot feature distribution before and after imputation

```{python}
color_pal = sns.color_palette(palette='muted')
def draw_histplot():
    f, axes = plt.subplots(nrows=len(null_features), ncols=5, figsize=(24, len(null_features)*6))
    for x in range(0, len(null_features)):
        sns.histplot(data_num, x=null_features[x], kde=True, ax=axes[x, 0], color=color_pal[0])
        sns.histplot(data_imp_mice, x=null_features[x], kde=True, ax=axes[x, 1], color=color_pal[1])
        sns.histplot(data_imp_knn, x=null_features[x], kde=True, ax=axes[x, 2], color=color_pal[2])
        sns.histplot(data_imp_mean, x=null_features[x], kde=True, ax=axes[x, 3], color=color_pal[3])
        sns.histplot(data_imp_median, x=null_features[x], kde=True, ax=axes[x, 4], color=color_pal[4])
    
    for i, ax in enumerate(axes.reshape(-1)):
        if i % 5 == 0:
            selected_title = 'Before Imputation'
            selected_data = data_num[null_features[int(i/5)]].dropna()
        elif i % 5 == 1:
            selected_title = 'Multiple Imputation'
            selected_data = data_imp_mice[null_features[int(i/5)]]
        elif i % 5 == 2:
            selected_title = 'KNN Imputation'
            selected_data = data_imp_knn[null_features[int(i/5)]]
        elif i % 5 == 3:
            selected_title = 'Mean Imputation'
            selected_data = data_imp_mean[null_features[int(i/5)]]
        elif i % 5 == 4:
            selected_title = 'Median Imputation'
            selected_data = data_imp_median[null_features[int(i/5)]]
        ax.set_title(selected_title)
        ax.text(x=0.97, y=0.97, transform=ax.transAxes, s="Skewness: %f" % skew(selected_data),\
            fontsize=9, verticalalignment='top', horizontalalignment='right')
        ax.text(x=0.97, y=0.91, transform=ax.transAxes, s="Kurtosis: %f" % kurtosis(selected_data),\
            fontsize=9, verticalalignment='top', horizontalalignment='right')
draw_histplot()
```

Code to compute skewness and kurtosis differences between feature distributions before and after imputation

#Creating dictionary that holds differences of skewness and kurtosis between data distribution per feature prior to imputation and after imputation
diff_dict=dict((k,{}) for k in null_features)
for k in null_features:
  knn_dist=data_imp_knn[k]
  mean_dist=data_imp_mean[k]
  median_dist=data_imp_median[k]
  mice_dist=data_imp_mice[k]
  before_dist=data_num[k].dropna()
  skew_knn=skew(before_dist)-skew(knn_dist) # computing the skew difference between feature distribution after KNN imputation and before imputation
  skew_mean=skew(before_dist)-skew(mean_dist) # computing the skew difference between feature distribution after mean imputation and before imputation
  skew_median=skew(before_dist)-skew(median_dist) # computing the skew difference between feature distribution after mean imputation and before imputation
  skew_mice=skew(before_dist)-skew(mice_dist) # computing the skew difference between feature distribution after multiple imputation and before imputation
  kurtosis_knn=kurtosis(before_dist)-kurtosis(knn_dist)  #computing the kurtosis difference between feature distribution after KNN imputation and before imputation
  kurtosis_mean=kurtosis(before_dist)-kurtosis(mean_dist) #computing the kurtosis difference between feature distribution after mean imputation and before imputation
  kurtosis_median=kurtosis(before_dist)-kurtosis(median_dist) #computing the kurtosis difference between feature distribution after median imputation and before imputation
  kurtosis_mice=kurtosis(before_dist)-kurtosis(mice_dist) #computing the kurtosis difference between feature distribution after multiple imputation and before imputation
  diff_dict[k]={**diff_dict[k],**{"KNN":(skew_knn,kurtosis_knn),"mean":(skew_mean,kurtosis_mean),"median":(skew_median,kurtosis_median),"mice":(skew_mice,kurtosis_mice)}} #grouping skew and kurtosis differences for all imputation methods for feature in dictionary
diff_dict
d=pd.DataFrame.from_dict(diff_dict, orient='index') #converting dictionary into Pandas DataFrame
# Converting DataFrame into tidy format
d['KNN_skew'], d['KNN_kurtosis'] = zip(*d.KNN)
d['mean_skew'], d['mean_kurtosis'] = zip(*d['mean'])
d['median_skew'], d['median_kurtosis'] = zip(*d['median'])
d['mice_skew'], d['mice_kurtosis'] = zip(*d.mice)
d.drop(columns=["KNN","mean","median","mice"],inplace=True) #dropping non-tidy columns
d #printing new dataframe
KNN_skew KNN_kurtosis mean_skew mean_kurtosis median_skew median_kurtosis mice_skew mice_kurtosis
life_expectancy 0.003273 -0.007734 0.001089 -0.009439 0.003785 -0.010385 0.001788 -0.006122
adult_mortality -0.002312 -0.011111 -0.002003 -0.016202 -0.003530 -0.017982 -0.003457 -0.011319
alcohol -0.016289 -0.076257 -0.020474 -0.155283 -0.060006 -0.177741 -0.011953 -0.022984
hepatitis_b 0.001497 -0.348235 0.212056 -1.335997 0.350902 -1.629737 -0.421941 1.707761
bmi -0.005635 -0.003758 0.001279 -0.020010 0.009842 -0.020094 -0.020041 0.011406
polio 0.003941 -0.029102 0.006814 -0.044053 0.010858 -0.051149 -0.029439 0.152438
total_expenditure -0.016264 -0.172079 -0.025249 -0.345994 -0.042427 -0.357587 -0.017734 -0.092385
diphtheria 0.005596 -0.033747 0.006731 -0.042634 0.010814 -0.049918 -0.041846 0.226023
gdp -0.272051 -2.409572 -0.276379 -2.753835 -0.337224 -2.809472 -0.275180 -2.420516
population -0.919674 -44.934991 -2.126174 -85.665905 -2.057870 -83.127646 -1.465561 -66.036475
thinness_10_19_years 0.007102 -0.004108 -0.009985 -0.081506 -0.018026 -0.089857 0.017748 0.075554
thinness_5_9_years 0.005887 -0.010074 -0.010369 -0.086044 -0.018271 -0.094371 0.013898 0.062154
income_composition_of_resources -0.031833 0.043169 0.033943 -0.264460 0.068763 -0.301006 0.001816 0.152764
schooling -0.016962 0.020542 0.017431 -0.228047 0.032617 -0.237329 0.136946 -0.206604

The best imputation method for most features is KNN imputation so weโ€™ll stick with this imputation method going forward. There was no case where median or mean imputation performed best.

Linear regression modelling

First model: single predictor model

Now, we turn our attention to modelling and weโ€™ll be building a first linear regression model for life_expectancy using a single predictor: income_composition_of_resources.

y_knn = data_imp_knn['life_expectancy'] ##Selecting the data that corresponds to our dependent variable
X_knn = data_imp_knn['income_composition_of_resources'] ##Selecting the data that corresponds to our independent variable

We build a linear regression model using the statsmodels library and compute a few summary metrics for our model:

mod = sm.OLS(y_knn, X_knn)
res = mod.fit()
ypred = res.predict(X_knn)

# calculate the rmse
rmse_mod = rmse(y_knn, ypred)
print('RMSE: ',rmse_mod)
print(res.summary()) #print summary metrics

#calculate and print the 95% confidence interval
print("\n95% confidence interval:\n", res.conf_int(0.05))
RMSE:  16.72575831404811
                                 OLS Regression Results                                
=======================================================================================
Dep. Variable:        life_expectancy   R-squared (uncentered):                   0.943
Model:                            OLS   Adj. R-squared (uncentered):              0.943
Method:                 Least Squares   F-statistic:                          4.834e+04
Date:                Mon, 13 May 2024   Prob (F-statistic):                        0.00
Time:                        19:42:14   Log-Likelihood:                         -12445.
No. Observations:                2938   AIC:                                  2.489e+04
Df Residuals:                    2937   BIC:                                  2.490e+04
Df Model:                           1                                                  
Covariance Type:            nonrobust                                                  
===================================================================================================
                                      coef    std err          t      P>|t|      [0.025      0.975]
---------------------------------------------------------------------------------------------------
income_composition_of_resources   102.9273      0.468    219.866      0.000     102.009     103.845
==============================================================================
Omnibus:                     1458.350   Durbin-Watson:                   0.366
Prob(Omnibus):                  0.000   Jarque-Bera (JB):             8557.027
Skew:                           2.350   Prob(JB):                         0.00
Kurtosis:                       9.915   Cond. No.                         1.00
==============================================================================

Notes:
[1] Rยฒ is computed without centering (uncentered) since the model does not contain a constant.
[2] Standard Errors assume that the covariance matrix of the errors is correctly specified.

95% confidence interval:
                                           0          1
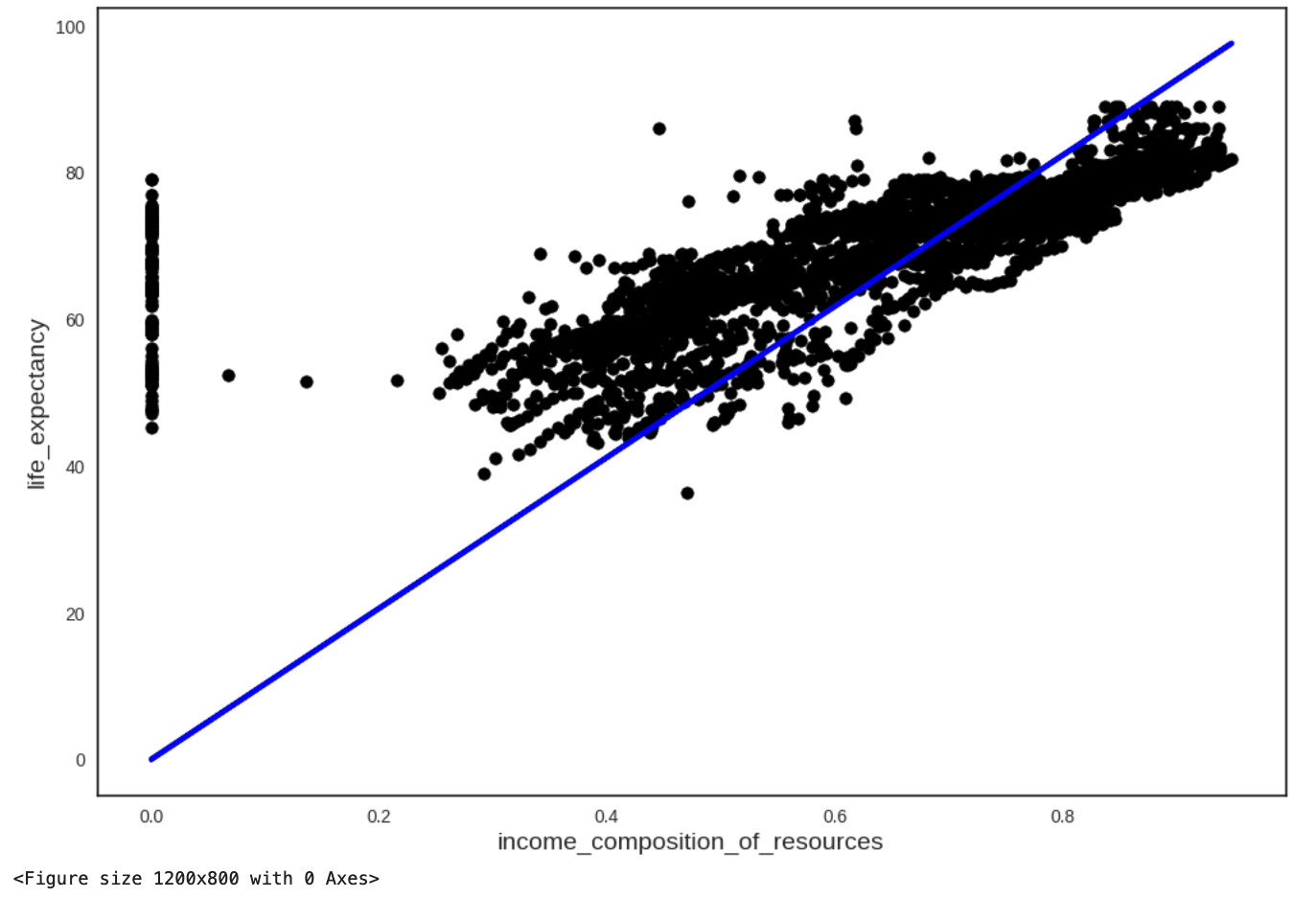
income_composition_of_resources  102.009374  103.84519

We visualise our model:

```{python}
plt.scatter(X_knn, y_knn, color="black")
plt.plot(X_knn, 102.9273*X_knn, color="blue", linewidth=3)

plt.xlabel("income_composition_of_resources")
plt.ylabel("life_expectancy")
plt.show()
plt.savefig("regression_1var_OLS.png",bbox_inches="tight")
```

Multivariate linear regression

In a similar fashion, we build models with multiple predictors. Our dependent variable stays unchanged here but our independent variables vary.

In our first try, we select income_composition_of_resources,adult_mortality,gdp,hiv_aids,thinness_10_19_years,diphtheria,bmi,alcohol and polio as predictors.

X_ind=data_imp_knn[['income_composition_of_resources','adult_mortality','gdp','hiv_aids','thinness_10_19_years','diphtheria','bmi','alcohol','polio']] #new independent variables
model = sm.OLS(y_knn, X_ind)
result = model.fit()
y_predicted = result.predict(X_ind)

# calc rmse
rmse_multivar = rmse(y_knn, y_predicted)
print("RMSE: ", rmse_multivar)
print(result.summary())
print("\n95% confidence interval:\n", result.conf_int(0.05))
RMSE:  9.75957572236227
                                 OLS Regression Results                                
=======================================================================================
Dep. Variable:        life_expectancy   R-squared (uncentered):                   0.980
Model:                            OLS   Adj. R-squared (uncentered):              0.980
Method:                 Least Squares   F-statistic:                          1.636e+04
Date:                Mon, 13 May 2024   Prob (F-statistic):                        0.00
Time:                        19:42:14   Log-Likelihood:                         -10862.
No. Observations:                2938   AIC:                                  2.174e+04
Df Residuals:                    2929   BIC:                                  2.180e+04
Df Model:                           9                                                  
Covariance Type:            nonrobust                                                  
===================================================================================================
                                      coef    std err          t      P>|t|      [0.025      0.975]
---------------------------------------------------------------------------------------------------
income_composition_of_resources    38.9115      1.097     35.470      0.000      36.760      41.062
adult_mortality                     0.0254      0.002     15.335      0.000       0.022       0.029
gdp                              6.661e-07   1.54e-05      0.043      0.965   -2.95e-05    3.08e-05
hiv_aids                           -0.5993      0.042    -14.288      0.000      -0.682      -0.517
thinness_10_19_years                1.0417      0.046     22.776      0.000       0.952       1.131
diphtheria                          0.1472      0.010     14.226      0.000       0.127       0.168
bmi                                 0.2209      0.011     19.909      0.000       0.199       0.243
alcohol                             0.3061      0.054      5.663      0.000       0.200       0.412
polio                               0.1615      0.010     15.662      0.000       0.141       0.182
==============================================================================
Omnibus:                      543.558   Durbin-Watson:                   0.794
Prob(Omnibus):                  0.000   Jarque-Bera (JB):             1114.455
Skew:                           1.090   Prob(JB):                    9.98e-243
Kurtosis:                       5.085   Cond. No.                     9.10e+04
==============================================================================

Notes:
[1] Rยฒ is computed without centering (uncentered) since the model does not contain a constant.
[2] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[3] The condition number is large, 9.1e+04. This might indicate that there are
strong multicollinearity or other numerical problems.

95% confidence interval:
                                          0          1
income_composition_of_resources  36.760496  41.062478
adult_mortality                   0.022184   0.028688
gdp                              -0.000030   0.000031
hiv_aids                         -0.681531  -0.517047
thinness_10_19_years              0.952026   1.131384
diphtheria                        0.126935   0.167521
bmi                               0.199179   0.242698
alcohol                           0.200144   0.412149
polio                             0.141239   0.181665

All variables come back as significant except for GDP, so we try another model that has gdp replaced with total_expenditure. This time, all variables come back significant.

X_ind=data_imp_knn[['income_composition_of_resources','adult_mortality','total_expenditure','hiv_aids','thinness_10_19_years','diphtheria','bmi','alcohol','polio']] #new independent variables
model = sm.OLS(y_knn, X_ind)
result = model.fit()
y_predicted = result.predict(X_ind)

# calc rmse
rmse_multivar = rmse(y_knn, y_predicted)
print("RMSE: ", rmse_multivar)
print(result.summary())
print("\n95% confidence interval:\n", result.conf_int(0.05))
RMSE:  9.212757334610943
                                 OLS Regression Results                                
=======================================================================================
Dep. Variable:        life_expectancy   R-squared (uncentered):                   0.983
Model:                            OLS   Adj. R-squared (uncentered):              0.983
Method:                 Least Squares   F-statistic:                          1.840e+04
Date:                Mon, 13 May 2024   Prob (F-statistic):                        0.00
Time:                        19:42:14   Log-Likelihood:                         -10693.
No. Observations:                2938   AIC:                                  2.140e+04
Df Residuals:                    2929   BIC:                                  2.146e+04
Df Model:                           9                                                  
Covariance Type:            nonrobust                                                  
===================================================================================================
                                      coef    std err          t      P>|t|      [0.025      0.975]
---------------------------------------------------------------------------------------------------
income_composition_of_resources    37.1246      1.009     36.783      0.000      35.146      39.104
adult_mortality                     0.0210      0.002     13.445      0.000       0.018       0.024
total_expenditure                   1.3447      0.071     18.921      0.000       1.205       1.484
hiv_aids                           -0.6377      0.040    -16.097      0.000      -0.715      -0.560
thinness_10_19_years                0.9971      0.043     23.154      0.000       0.913       1.082
diphtheria                          0.1252      0.010     12.733      0.000       0.106       0.144
bmi                                 0.1801      0.011     16.834      0.000       0.159       0.201
alcohol                             0.1187      0.052      2.301      0.021       0.018       0.220
polio                               0.1439      0.010     14.722      0.000       0.125       0.163
==============================================================================
Omnibus:                      473.872   Durbin-Watson:                   0.784
Prob(Omnibus):                  0.000   Jarque-Bera (JB):              938.828
Skew:                           0.976   Prob(JB):                    1.37e-204
Kurtosis:                       4.964   Cond. No.                     1.36e+03
==============================================================================

Notes:
[1] Rยฒ is computed without centering (uncentered) since the model does not contain a constant.
[2] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[3] The condition number is large, 1.36e+03. This might indicate that there are
strong multicollinearity or other numerical problems.

95% confidence interval:
                                          0          1
income_composition_of_resources  35.145660  39.103615
adult_mortality                   0.017952   0.024083
total_expenditure                 1.205311   1.483997
hiv_aids                         -0.715405  -0.560039
thinness_10_19_years              0.912662   1.081536
diphtheria                        0.105914   0.144472
bmi                               0.159084   0.201029
alcohol                           0.017551   0.219826
polio                             0.124742   0.163076

Footnotes

  1. Make sure you have the blosc version at least 1.11.1 installed when you use miceforest. To check package versions, you can use the command conda list or pip list on the terminal, command line prompt or powershellโ†ฉ๏ธŽ