🗓️ Week 02:
Linear Regression

DS202 Data Science for Social Scientists

Dr. Jon Cardoso-Silva

@LSEDataScience

10/7/22

What we will cover today

• What is Linear Regression
• Regression coefficients
• Residual errors
• Ordinary Least Squares
• Confidence Intervals
• Hypothesis Testing
• What’s Next

What is Linear Regression

The basic models

Linear regression is a simple approach to supervised learning.

The generic supervised model:

\[ Y = \operatorname{f}(X) + \epsilon \]

is defined more explicitly as follows ➡️

Simple linear regression

\[ \begin{align} Y = \beta_0 +& \beta_1 X + \epsilon, \\ \\ \\ \end{align} \]

when we use a single predictor, \(X\).

Multiple linear regression

\[ \begin{align} Y = \beta_0 &+ \beta_1 X_1 + \beta_2 X_2 \\ &+ \dots \\ &+ \beta_p X_p + \epsilon \end{align} \]

when there are multiple predictors, \(X_p\).

Warning

• True regression functions are never linear!
• Although it may seem overly simplistic, linear regression is extremely useful both conceptually and practically.

• See 📺 Regression: Crash Course Statistics on YouTube for inspiration on how to present linear regression to students.

• We will talk about both types of models, how we can estimate the values of all \(\beta\) and assess how good our models are.

Regression coefficients

Linear Regression with a single predictor

We assume a model:

\[ Y = \beta_0 + \beta_1 X + \epsilon , \]

where:

• \(\beta_0\): an unknown constant that represents the intercept of the line.
• \(\beta_1\): an unknown constant that represents the slope of the line
• \(\epsilon\): the random error term (irreducible)

\(\beta_0\) and \(\beta_1\) are also known as coefficients or parameters of the model.

Linear Regression with a single predictor

We want to estimate:

\[ \hat{y} = \hat{\beta_0} + \hat{\beta_1} x \]

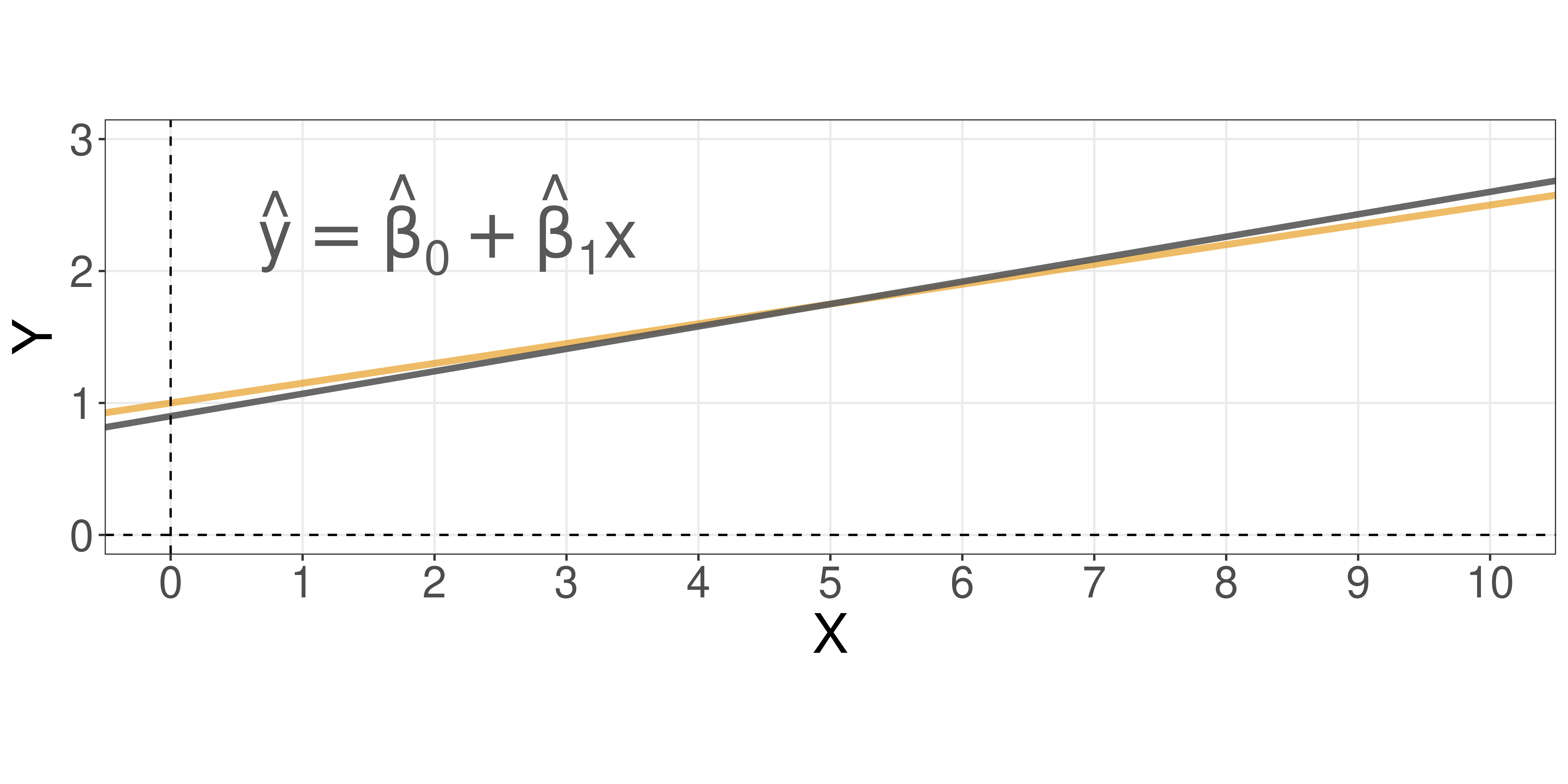
where:

• \(\hat{y}\): is a prediction of \(Y\) on the basis of \(X = x\).
• \(\hat{\beta_0}\): is an estimate of the “true” \(\beta_0\).
• \(\hat{\beta_1}\): is an estimate of the “true” \(\beta_1\).

The hat symbol denotes an estimated value.

Different estimators, different equations

There are multiple ways to estimate the coefficients.

• If you use different techniques, you might get different equations
• The most common algorithm is called
  Ordinary Least Squares (OLS)
• Just to name a few other estimators (Karafiath 2009):
  • Least Absolute Deviation (LAD)
  • Weighted Least Squares (WLS)
  • Generalized Least Squares (GLS)
  • Heteroskedastic-Consistent (HC) variants

We will only cover OLS in this course.

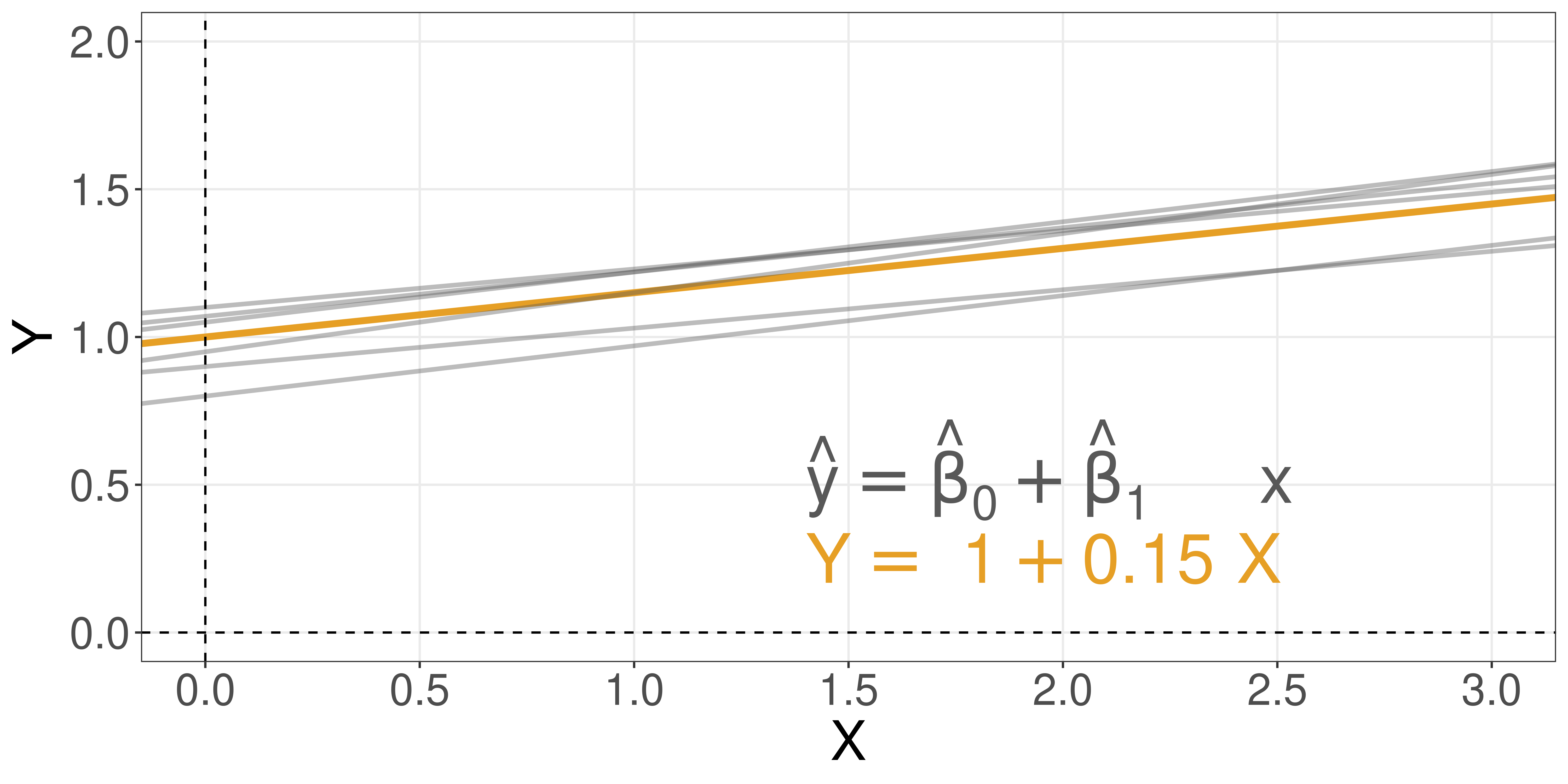
Residual errors

To understand the Ordinary Least Squares method, we first need to understand the concept of residuals.

The concept of residuals

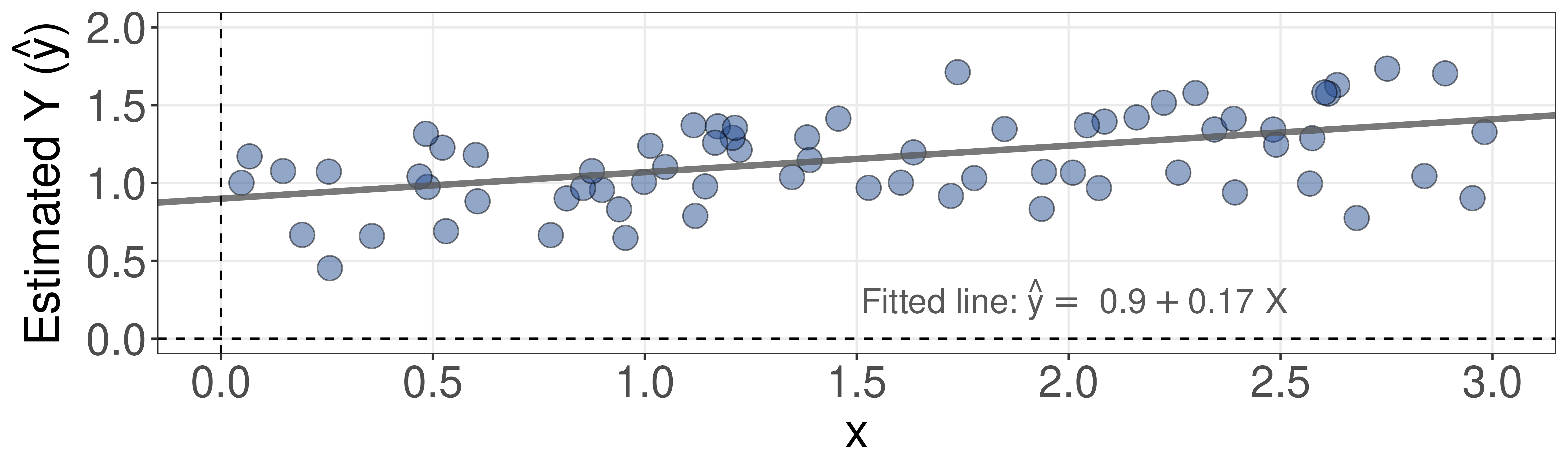
Suppose you came across some data:

First, let’s think of the concept of residuals…

And you suspect there is a linear relationship between X and Y.

The concept of residuals

So, you decide to fit a line to it.

A line that goes right through the middle of the cloud of data.

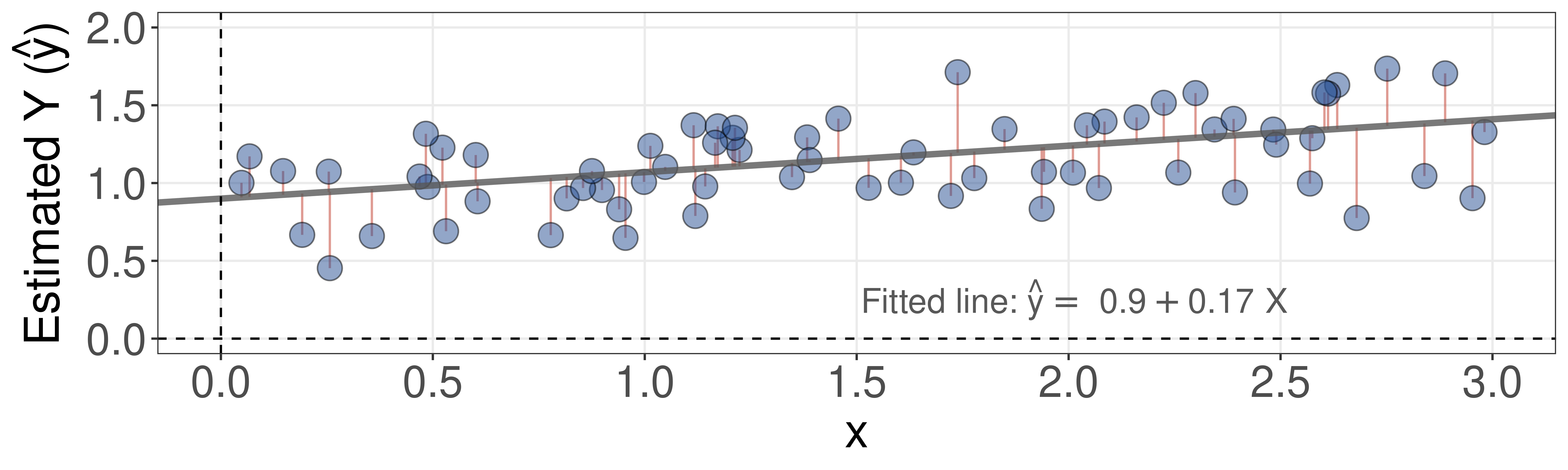
The concept of residuals

Residuals are the distances from each data point to this line.

\(e_i\)\(=y_i-\hat{y}_i\) represents the \(i\)th residual

Residual Sum of Squares (RSS)

From this, we can define the Residual Sum of Squares (RSS) as

\[ \mathrm{RSS}= e_1^2 + e_2^2 + \dots + e_n^2, \]

or equivalently as

\[ \mathrm{RSS}= (y_1 - \hat{\beta}_0 - \hat{\beta}_1 x_1)^2 + (y_2 - \hat{\beta}_0 - \hat{\beta}_1 x_2)^2 + \dots + (y_n - \hat{\beta}_0 - \hat{\beta}_1 x_n)^2. \]

Note

The (ordinary) least squares approach chooses \(\hat{\beta}_0\) and \(\hat{\beta}_1\) to minimize the RSS.

That is how it does its job.

A question for you

Why the squares and not, say, just the sum of residuals?

• Explain that the sum penalizes individual large errors a lot more Consider adding a visualisation to illustrate this point.

Ordinary Least Squares

How do we estimate the coefficients using the ordinary least squares algorithm?

The objective function

We treat this as an optimisation problem. We want to minimize RSS: \[ \begin{align} \min \mathrm{RSS} =& \sum_i^n{e_i^2} \\ =& \sum_i^n{\left(y_i - \hat{y}_i\right)^2} \\ =& \sum_i^n{\left(y_i - \hat{\beta}_0 - \hat{\beta}_1 x_i\right)^2} \end{align} \]

Estimating \(\hat{\beta}_0\)

To find \(\hat{\beta}_0\), we have to solve the following partial derivative:

\[ \frac{\partial ~\mathrm{RSS}}{\partial \hat{\beta}_0}{\sum_i^n{(y_i - \hat{\beta}_0 - \hat{\beta}_1 x_i)^2}} = 0 \]

… which will lead you to:

\[ \hat{\beta}_0 = \bar{y} - \hat{\beta}_1 \bar{x}, \]

where we made use of the sample means:

• \(\bar{y} \equiv \frac{1}{n} \sum_{i=1}^n y_i\)
• \(\bar{x} \equiv \frac{1}{n} \sum_{i=1}^n x_i\)

Full derivation if needed:

\[ \begin{align} 0 &= \frac{\partial ~\mathrm{RSS}}{\partial \hat{\beta}_0}{\sum_i^n{(y_i - \hat{\beta}_0 - \hat{\beta}_1 x_i)^2}} & (\text{chain rule})\\ 0 &= \sum_i^n{-2 (y_i - \hat{\beta}_0 - \hat{\beta}_1 x_i)} & (\text{take $-2$ out})\\ 0 &= -2 \sum_i^n{ (y_i - \hat{\beta}_0 - \hat{\beta}_1 x_i)} & (\div -2) \\ 0 &=\sum_i^n{ (y_i - \hat{\beta}_0 - \hat{\beta}_1 x_i)} & (\text{sep. sums}) \\ 0 &=\sum_i^n{y_i} - \sum_i^n{\hat{\beta}_0} - \sum_i^n{\hat{\beta}_1 x_i} & (\text{simplify}) \\ 0 &=\sum_i^n{y_i} - n\hat{\beta}_0 - \hat{\beta}_1\sum_i^n{ x_i} & (+ n\hat{\beta}_0) \\ n\hat{\beta}_0 &= \sum_i^n{y_i} - \hat{\beta}_1\sum_i^n{ x_i} & (\text{isolate }\hat{\beta}_0 ) \\ \hat{\beta}_0 &= \frac{\sum_i^n{y_i} - \hat{\beta}_1\sum_i^n{ x_i}}{n} & (\text{rearranging}) \\ \hat{\beta}_0 &= \frac{\sum_i^n{y_i}}{n} - \hat{\beta}_1\frac{\sum_i^n{x_i}}{n} & (\text{or simply}) \\ \hat{\beta}_0 &= \bar{y} - \hat{\beta}_1 \bar{x} & \blacksquare \end{align} \]

📝 Give it a go! Pretend \(\hat{\beta}_1\) is constant and use the power rule to solve the equation and reach the same result.

Estimating \(\hat{\beta}_1\)

Similarly, to find \(\hat{\beta}_1\) we solve:

\[ \frac{\partial ~\mathrm{RSS}}{\partial \hat{\beta}_1}{[\sum_i^n{y_i - \hat{\beta}_0 - \hat{\beta}_1 x_i}]} = 0 \]

… which will lead you to:

\[ \hat{\beta}_1 = \frac{\sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y})}{\sum_{i=1}^n (x_i-\bar{x})^2} \]

Full derivation if needed:

\[ \begin{align} 0 &= \frac{\partial ~\mathrm{RSS}}{\partial \hat{\beta}_1}{\sum_i^n{(y_i - \hat{\beta}_0 - \hat{\beta}_1 x_i)^2}} & (\text{chain rule})\\ 0 &= \sum_i^n{\left(-2x_i~ (y_i - \hat{\beta}_0 - \hat{\beta}_1 x_i)\right)} & (\text{take $-2$ out})\\ 0 &= -2\sum_i^n{\left( x_i~ (y_i - \hat{\beta}_0 - \hat{\beta}_1 x_i)\right)} & (\div -2) \\ 0 &= \sum_i^n{\left(x_i~ (y_i - \hat{\beta}_0 - \hat{\beta}_1 x_i)\right)} & (\text{distribute } x_i) \\ 0 &= \sum_i^n{\left(y_ix_i - \hat{\beta}_0x_i - \hat{\beta}_1 x_i^2\right)} & (\text{replace } \hat{\beta}_0) \\ 0 &= \sum_i^n{\left(y_ix_i - (\bar{y} - \hat{\beta}_1 \bar{x})x_i - \hat{\beta}_1 x_i^2\right)} & (\text{rearrange}) \\ 0 &= \sum_i^n{\left(y_ix_i - \bar{y}x_i + \hat{\beta}_1 \bar{x}x_i - \hat{\beta}_1 x_i^2\right)} & (\text{separate sums}) \\ 0 &= \sum_i^n{\left(y_ix_i - \bar{y}x_i\right)} + \sum_i^n{\left(\hat{\beta}_1 \bar{x}x_i - \hat{\beta}_1 x_i^2\right)} & (\text{take $\hat{\beta}_1$ out}) \\ 0 &= \sum_i^n{\left(y_ix_i - \bar{y}x_i\right)} + \hat{\beta}_1\sum_i^n{\left(\bar{x}x_i - x_i^2\right)} & (\text{isolate}) \\ \hat{\beta}_1 &= \frac{\sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y})}{\sum_{i=1}^n (x_i-\bar{x})^2} \end{align} \]

📝 Give it a go! Use the same method as before to solve the equation and isolate \(\hat{\beta}_1\). Tip: Use the previous formula to substitute \(\hat{\beta}_0\).

Parameter Estimation (OLS)

And that is how OLS works!

\[ \begin{align} \hat{\beta}_1 &= \frac{\sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y})}{\sum_{i=1}^n (x_i-\bar{x})^2} \\ \hat{\beta}_0 &= \bar{y} - \hat{\beta}_1 \bar{x} \end{align} \]

Estimates for Multiple Regression

The process of estimation is similar when we have more than one predictor. To estimate:

\[ \hat{y} = \hat{\beta}_0 + \hat{\beta}_1 x_1 + \hat{\beta}_2 x_2 + \dots + \hat{\beta}_p x_p. \]

We aim to minimize Residual Sum of Squares as before:

\[ \min \mathrm{RSS} = \sum_{i=1}^n (y_i - \hat{y}_i)^2 = \sum_{i=1}^n (y_i - \hat{\beta}_0 - \hat{\beta}_1 x_{i1} - \hat{\beta}_2 x_{i2} - \dots - \hat{\beta}_p x_{ip})^2. \]

This is done using standard statistical software — you need a good linear algebra solver.

The values \(\hat{\beta}_0, \hat{\beta}_1, \dots, \hat{\beta}_p\) that minimize RSS are the multiple least squares regression coefficient estimates.

Example: Advertising data

A sample of the data:

library(tidyverse)

file = "https://www.statlearning.com/s/Advertising.csv"
advertising <- read_csv(file) %>% select(-1)
head(advertising, 11)

# A tibble: 11 × 4
      TV radio newspaper sales
   <dbl> <dbl>     <dbl> <dbl>
 1 230.   37.8      69.2  22.1
 2  44.5  39.3      45.1  10.4
 3  17.2  45.9      69.3   9.3
 4 152.   41.3      58.5  18.5
 5 181.   10.8      58.4  12.9
 6   8.7  48.9      75     7.2
 7  57.5  32.8      23.5  11.8
 8 120.   19.6      11.6  13.2
 9   8.6   2.1       1     4.8
10 200.    2.6      21.2  10.6
11  66.1   5.8      24.2   8.6

How the data is spread:

summary(advertising$TV)

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
   0.70   74.38  149.75  147.04  218.82  296.40 

summary(advertising$radio)

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  0.000   9.975  22.900  23.264  36.525  49.600 

summary(advertising$newspaper)

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
   0.30   12.75   25.75   30.55   45.10  114.00 

summary(advertising$sales)

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
   1.60   10.38   12.90   14.02   17.40   27.00 

Relationship: advertising budget and sales

Is advertising spending related to sales?

This is the plot you see in the book (James et al. 2021, chap. 3)

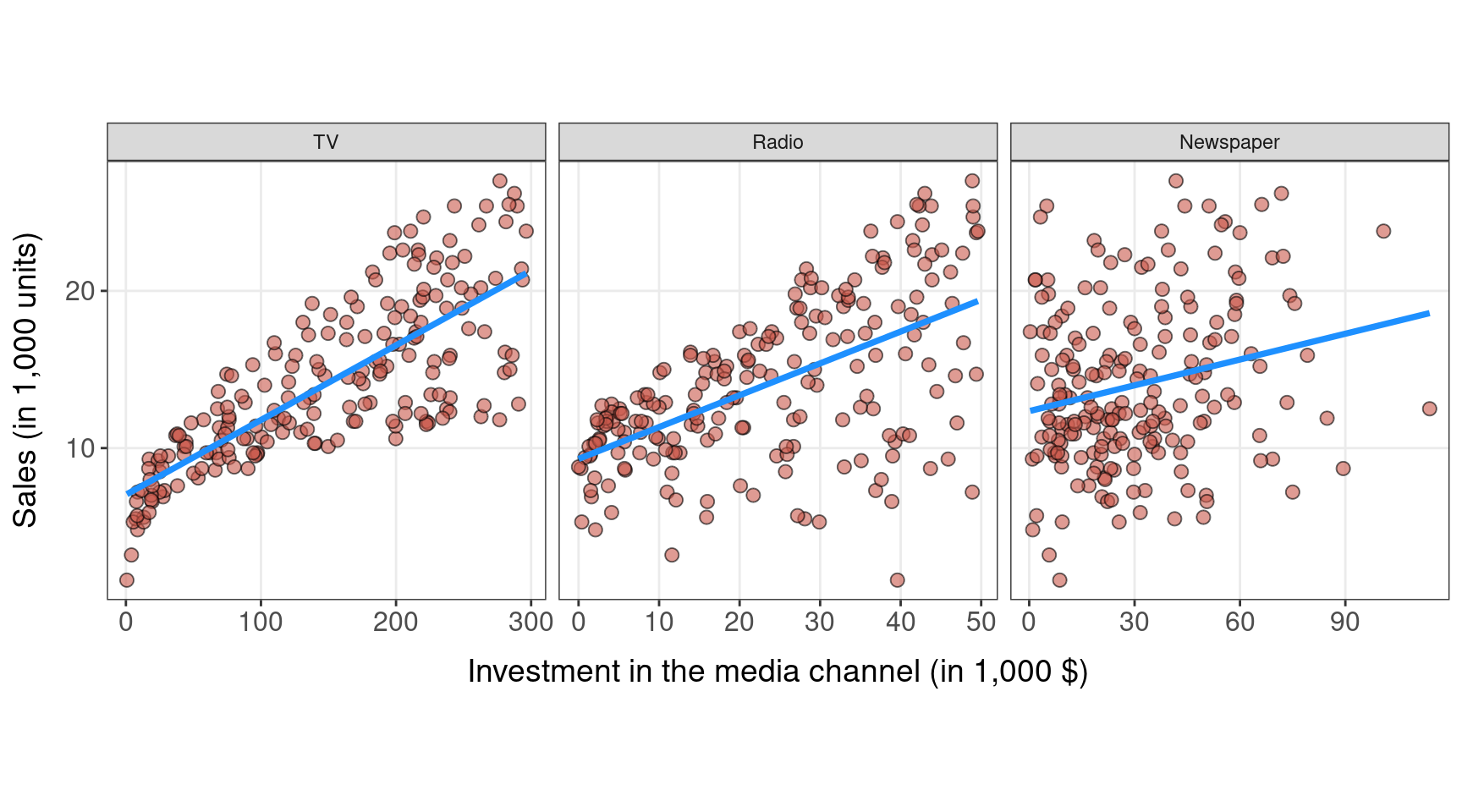
Relationship: advertising budget and sales

Is advertising spending related to sales?

This is the same plot but now all scales match

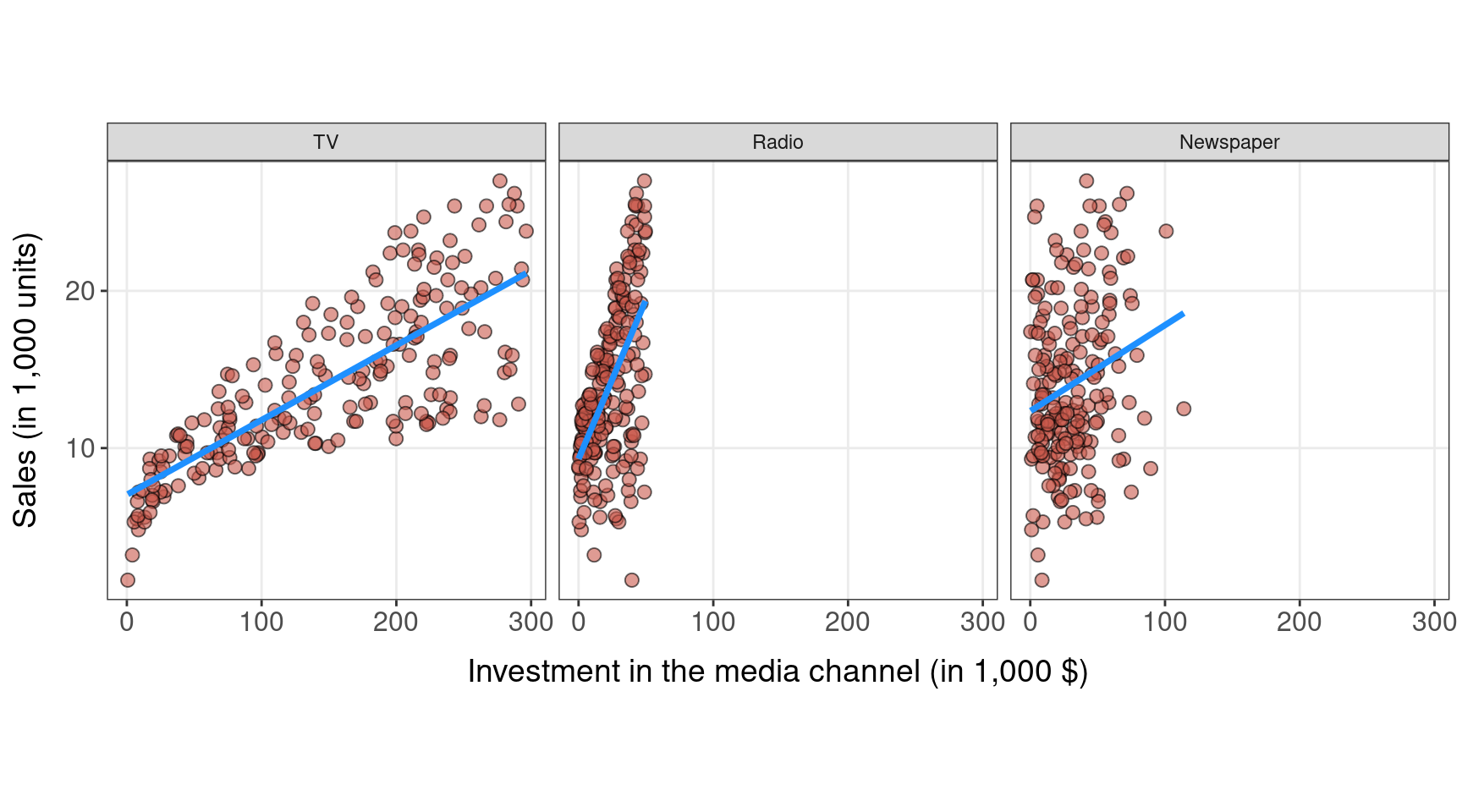
Simple linear regression models

• TV 📺

tv_model <- lm(sales ~ TV, data=advertising)
cat(sprintf("Sales (1k units) = %.4f %+.4f TV ($ 1k)\n", 
            tv_model$coefficients["(Intercept)"], 
            tv_model$coefficients["TV"]))

Sales (1k units) = 7.0326 +0.0475 TV ($ 1k)

• Radio 📻

radio_model <- lm(sales ~ radio, data=advertising)
cat(sprintf("Sales (1k units) = %.4f %+.4f Radio ($ 1k)\n", 
            radio_model$coefficients["(Intercept)"], 
            radio_model$coefficients["radio"]))

Sales (1k units) = 9.3116 +0.2025 Radio ($ 1k)

• Newspaper 📰

newspaper_model <- lm(sales ~ newspaper, data=advertising)
cat(sprintf("Sales (1k units) = %.4f %+.4f Newspaper ($ 1k)\n", 
            newspaper_model$coefficients["(Intercept)"], 
            newspaper_model$coefficients["newspaper"]))

Sales (1k units) = 12.3514 +0.0547 Newspaper ($ 1k)

🗨️ How should we interpret these models?

• Gather answers from students.
• For every 1k dollars spent in advertising on a particular media channel, we expect more \(\hat{\beta}_1\) thousand units of the product to be sold.
• Why don’t the models agree about the intercept?

Confidence Intervals

• If we were to fit a linear model from repeated samples of the data, we would get different coefficients every time.
• Because of the Central Limit Theorem, we know that the mean of this sampling distribution can be approximated by a Normal Distribution.
• We know from Normal Theory that 95% of the distribution lies within two times the standard deviation (centered around the mean).
  

A 95% confidence interval is defined as a range of values such that with 95% probability, the range will contain the true unknown value of the parameter.

• How well does my model fit the data?
• What is the confidence interval of the estimates? (under a scenario where we got repeated samples like the present sample).

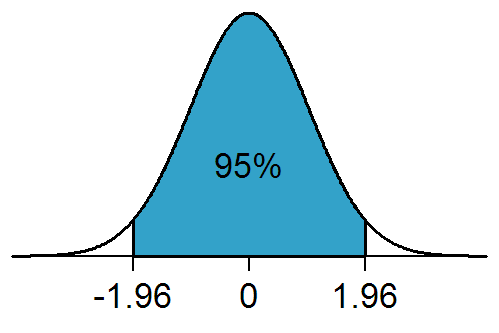
Confidence Interval of coefficients

• The confidence interval of an estimate has the form: \[ \hat{\beta}_1 \pm 2 \times \mathrm{SE}(\hat{\beta}_1). \] where \(SE\) is the standard error and reflects how the estimate varies under repeated sampling.

• That is, there is approximately a 95% chance that the interval \[ \biggl[ \hat{\beta}_1 - 2 \times \mathrm{SE}(\hat{\beta}_1), \hat{\beta}_1 + 2 \times \mathrm{SE}(\hat{\beta}_1) \biggr] \] will contain the true value of \(\beta_1\).

How SE differs from STD? See (Altman and Bland 2005)

Standard Errors

The standard error of \(\hat{\beta}_0\) and \(\hat{\beta}_1\) is shown below:

\[ \begin{align} \mathrm{SE}(\hat{\beta}_1)^2 &= \frac{\sigma^2}{\sum_{i=1}^n (x_i - \bar{x})^2}, \\ \mathrm{SE}(\hat{\beta}_0)^2 &= \sigma^2 \biggl[ \frac{1}{n} + \frac{\bar{x}^2}{\sum_{i=1}^n (x_i - \bar{x})^2} \biggr], \end{align} \]

where \(\sigma^2 = \operatorname{Var}(\epsilon)\).

• But, wait, we don’t know \(\epsilon\)! How would we compute \(\sigma^2\)?
• In practice, we aproximate \(\sigma^2 \approx \mathrm{RSE} = \sqrt{\mathrm{RSS}/(n-2)}\).

Important

💡 Standard errors are a type of standard deviation but are not the same! See (Altman and Bland 2005) for more on this.

• These formulas are only valid if we assume the errors \(\epsilon_i\) have common variance \(\sigma^2\) and are uncorrelated.
• RSE makes a comeback in Section 3.1.3

Back to our Advertising linear models

What are the confidence intervals of our independent linear models?

• TV 📺

confint(tv_model)

                 2.5 %     97.5 %
(Intercept) 6.12971927 7.93546783
TV          0.04223072 0.05284256

• Radio 📻

confint(radio_model)

                2.5 %     97.5 %
(Intercept) 8.2015885 10.4216877
radio       0.1622443  0.2427472

• Newspaper 📰

confint(newspaper_model)

                  2.5 %      97.5 %
(Intercept) 11.12595560 13.57685854
newspaper    0.02200549  0.08738071

🗨️ What does it mean?

• For every additional $1000 invested in Radio, we can expect an increase in sales of between 162 and 242 units.

Use the function confint to compute confidence intervals in R.

Hypothesis Testing

• Standard errors can also be used to perform hypothesis tests on the coefficients.
• The most common hypothesis test involves testing the null hypothesis of:
  • \(H_0\): There is no relationship between \(X\) and \(Y\) versus the .
  • \(H_A\): There is some relationship between \(X\) and \(Y\).

• Mathematically, this corresponds to testing:

\[ \begin{align} &~~~~H_0:&\beta_1 &= 0 \\ &\text{vs} \\ &~~~~H_A:& \beta_1 &\neq 0, \end{align} \]

since if \(\beta_1=0\) then the model reduces to \(Y = \beta_0 + \epsilon\), and \(X\) and \(Y\) are not associated.

p-values

• To test the null hypothesis, we compute a t-statistic, given by \[ t = \frac{\hat{\beta}_1 - 0}{\mathrm{SE}(\hat{\beta}_1)}, \]
• This will have a t-distribution¹ with \(n - 2\) degrees of freedom, assuming \(\beta_1 = 0\).
• Using statistical software, it is easy to compute the probability of observing any value equal to \(\mid t \mid\) or larger.
• We call this probability the p-value.

1. 🤔 How are the t-distribution and the Normal distribution related? Check this link to find out.

Back to our Advertising linear models

How significant are the linear models?

• TV 📺

out <- capture.output(summary(tv_model))
cat(paste(out[9:15]), sep="\n")

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 7.032594   0.457843   15.36   <2e-16 ***
TV          0.047537   0.002691   17.67   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

• Radio 📻

out <- capture.output(summary(radio_model))
cat(paste(out[9:15]), sep="\n")

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  9.31164    0.56290  16.542   <2e-16 ***
radio        0.20250    0.02041   9.921   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

• Newspaper 📰

out <- capture.output(summary(newspaper_model))
cat(paste(out[9:15]), sep="\n")

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 12.35141    0.62142   19.88  < 2e-16 ***
newspaper    0.05469    0.01658    3.30  0.00115 ** 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

🗨️ What does it mean?

What’s Next

After our 10-min break ☕:

• Metrics to assess goodness-of-fit
• Interpreting Multiple Linear Regression 📈
• Interaction effects
• Outliers
• Collinearity
• What will happen in our 💻 labs this week?

References

Altman, Douglas G, and J Martin Bland. 2005. “Standard Deviations and Standard Errors.” BMJ 331 (7521): 903. https://doi.org/10.1136/bmj.331.7521.903.

James, Gareth, Daniela Witten, Trevor Hastie, and Robert Tibshirani. 2021. An Introduction to Statistical Learning: With Applications in R. Second edition. Springer Texts in Statistics. New York NY: Springer. https://www.statlearning.com/.

Karafiath, Imre. 2009. “Is There a Viable Alternative to Ordinary Least Squares Regression When Security Abnormal Returns Are the Dependent Variable?” Review of Quantitative Finance and Accounting 32 (1): 17–31. https://doi.org/10.1007/s11156-007-0079-y.