✅ LSE DS202A 2025: Week 08 - Solutions
Note: You can access the executable version of this file on Nuvolos is you want to try things out for yourselves!
Week 8 Labs - Clustering Analysis in R (DS202)
Overview (90 minutes total)
Today we’ll explore different clustering algorithms and evaluation methods using Multiple Correspondence Analysis (MCA) coordinates (these coordinates were produced in Part II of last week’s lab based on World Values Survey data - you can review this part to see how the coordinates were generated). We’ll compare k-means variants, k-medoids, and DBSCAN clustering approaches.
Technical Skills: Implement k-means, k-medoids, and DBSCAN algorithms with evaluation methods (elbow, silhouette) and adapt code templates across different clustering approaches
Analytical Skills: Compare clustering methods, evaluate their appropriateness for datasets, and interpret metrics to determine optimal cluster numbers and trade-offs
Critical Thinking: Justify algorithm selection based on data characteristics, assess outlier treatment decisions, and critique clustering limitations
Practical Application: Design complete clustering workflows, troubleshoot parameter selection challenges, and communicate results through effective visualizations
Lab Structure:
- 10 min: Clustering algorithms overview + k-means template
- 50 min: Student exploration of algorithms and evaluation methods
- 30 min: DBSCAN exploration
Part 1: Introduction to Clustering Algorithms (10 minutes)
Key Differences Between Clustering Methods
| Algorithm | Centers | Distance | Outlier Sensitivity | Use Case |
|---|---|---|---|---|
| k-means | Computed centroids | Euclidean | High | Spherical clusters |
| k-means++ | Smart initialization | Euclidean | High | Better initial centroids |
| k-medoids | Actual data points | Any metric | Low | Non-spherical clusters |
| DBSCAN | None (density-based) | Any metric | Very low | Arbitrary shapes |
Setup
library(tidyverse)
library(cluster)
library(fpc)
library(dbscan)
library(broom)
library(patchwork)
# Load the MCA coordinates
mca_coords <- read_csv("data/mca-week-7.csv")Part 2: K-means Template & Algorithm Applications (50 minutes)
Step 1: Study the K-means Template (15 minutes)
Here’s the complete workflow for k-means clustering evaluation:
set.seed(123)
# k-means evaluation with both Elbow and Silhouette methods
mca_coords |>
select(dim_1:dim_2) |>
nest(data = everything()) |>
crossing(k = 2:10) |>
mutate(
kmeans_result = map2(
data,
k,
~ kmeans(.x, centers = .y)
),
glanced = map(kmeans_result, ~ broom::glance(.x)),
silhouette = map2_dbl(
data,
kmeans_result,
~ {
sil <- silhouette(.y$cluster, dist(.x))
mean(sil[, 3])
}
)
) |>
unnest(glanced) |>
select(k, tot.withinss, silhouette) |>
pivot_longer(c(tot.withinss, silhouette), names_to = "metric") |>
mutate(
metric = if_else(
metric == "tot.withinss",
"Elbow Method (minimize)",
"Silhouette Width (maximize)"
)
) |>
ggplot(aes(k, value)) +
facet_wrap(. ~ metric, scales = "free_y") +
geom_point() +
geom_line(linetype = "dashed") +
scale_x_continuous(breaks = 2:10) +
theme_minimal() +
labs(title = "k-means Cluster Evaluation")
# Create final clustering with chosen k
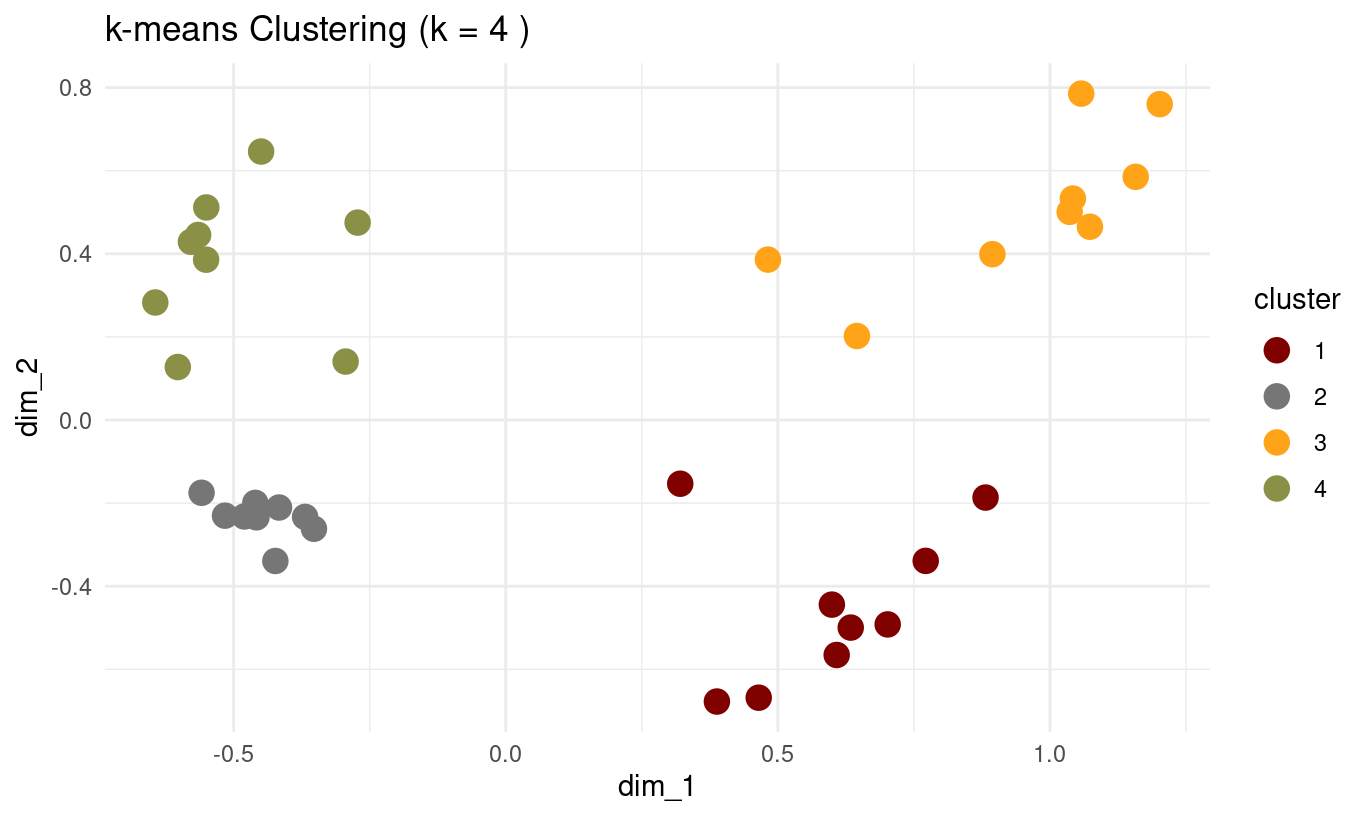
set.seed(123)
optimal_k <- 4 # Choose based on your evaluation plots
final_kmeans <- kmeans(mca_coords[, 1:2], centers = optimal_k, nstart = 25)
# Visualize final clustering
mca_coords |>
mutate(cluster = as.factor(final_kmeans$cluster)) |>
ggplot(aes(dim_1, dim_2, colour = cluster)) +
geom_point(size = 4) +
ggtitle(paste("k-means Clustering (k =", optimal_k, ")")) +
theme_minimal() +
ggsci::scale_colour_uchicago()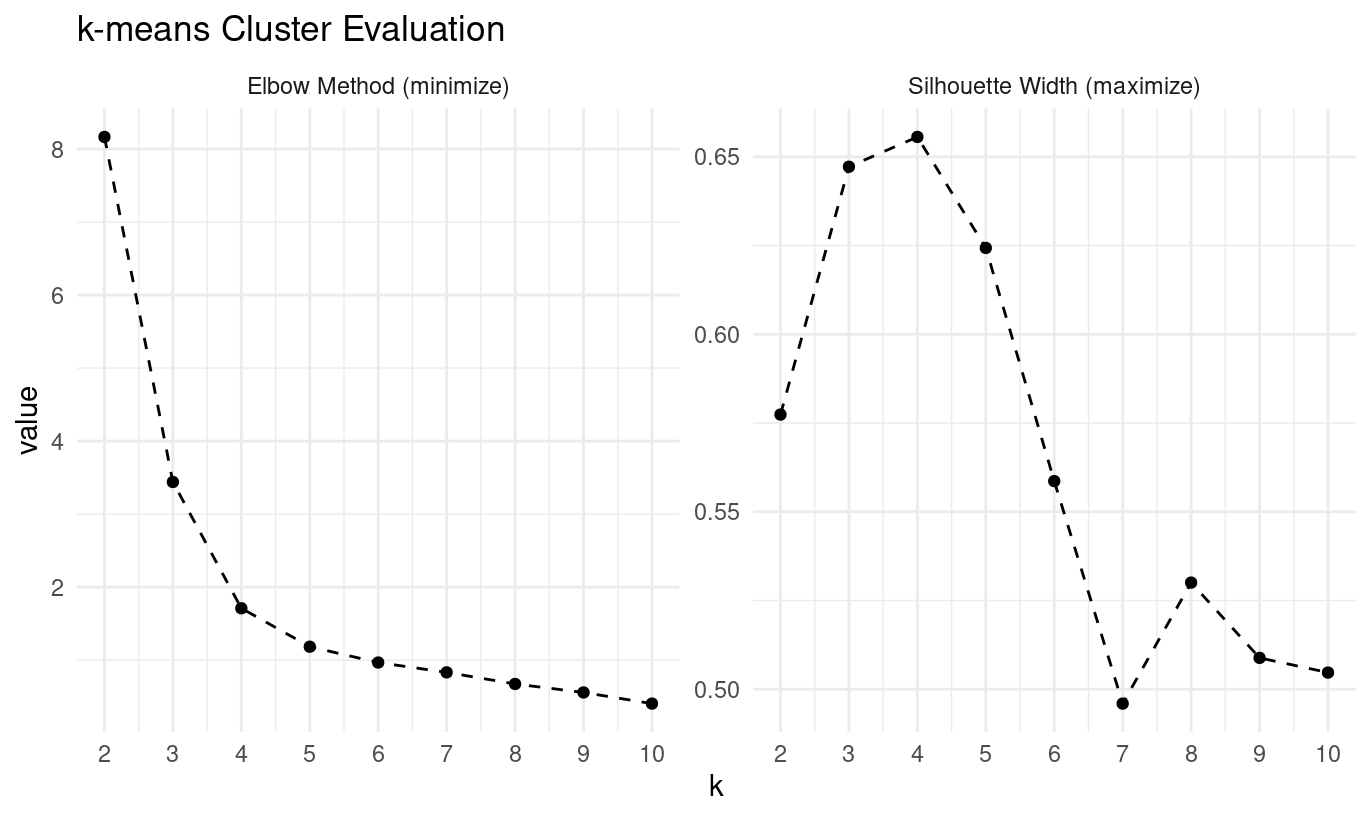
Quick Study Questions:
- What does
crossing(k = 2:10)create?
It creates a tibble containing every combination of the nested dataset and each value of k from 2 to 10 — essentially instructing R to run clustering for each value of k.
- Why do we use
map2()in the clustering step?
Because we must simultaneously provide two inputs for each iteration:
- the dataset (
data) and - the chosen value of k.
map2()lets us loop over both in parallel.
What are the two evaluation methods being calculated?
Elbow method via the total within-cluster sum of squares (
tot.withinss)Silhouette width for assessing separation quality
Step 2: Apply to K-medoids (15 minutes)
Your Task: Adapt the k-means template for k-medoids clustering.
set.seed(123)
mca_coords |>
select(dim_1:dim_2) |>
nest(data = everything()) |>
crossing(k = 2:10) |>
mutate(
pam_result = map2(data, k, ~ pam(.x, k = .y)),
glanced = map(
pam_result,
~ tibble(
tot.withinss = .x$objective[2], # Total cost from PAM
k = .x$k
)
),
silhouette = map2(
data,
pam_result,
~ {
sil <- silhouette(.y$clustering, dist(.x))
mean(sil[, 3])
}
)
) |>
unnest(c(glanced, silhouette)) |>
pivot_longer(c(tot.withinss, silhouette), names_to = "metric") |>
mutate(
metric = if_else(
metric == "tot.withinss",
"Elbow Method (minimize)",
"Silhouette Width (maximize)"
)
) |>
ggplot(aes(k, value)) +
facet_wrap(. ~ metric, scales = "free_y") +
geom_point() +
geom_line(linetype = "dashed") +
scale_x_continuous(breaks = 2:10) +
theme_minimal()
# Run k-medoids clustering
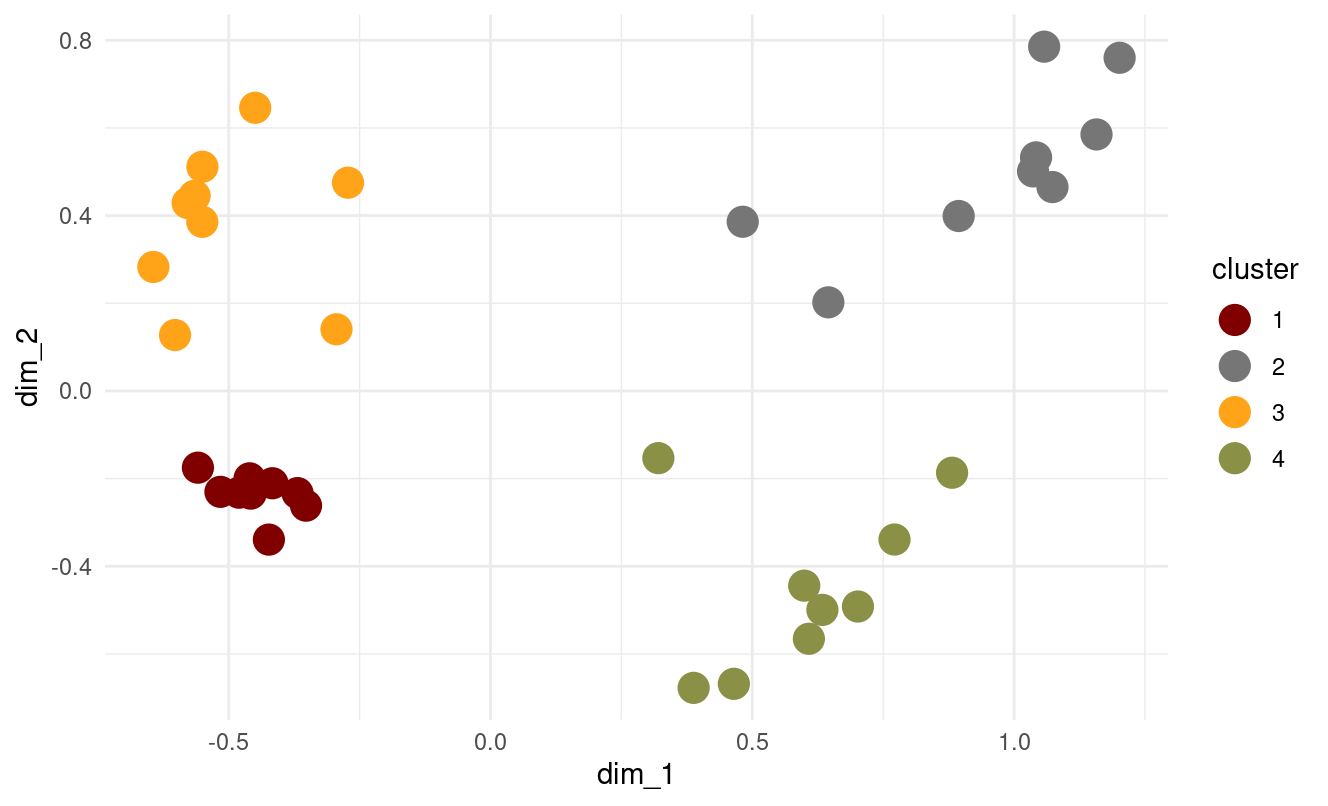
set.seed(123)
kmedoids_result <- pam(mca_coords[, 1:2], k = 4)
clusters_medoids <- kmedoids_result$clustering
# Plot the results
mca_coords |>
mutate(cluster = as.factor(clusters_medoids)) |>
ggplot(aes(dim_1, dim_2, colour = cluster)) +
geom_point(size = 5) +
theme_minimal() +
ggsci::scale_colour_uchicago()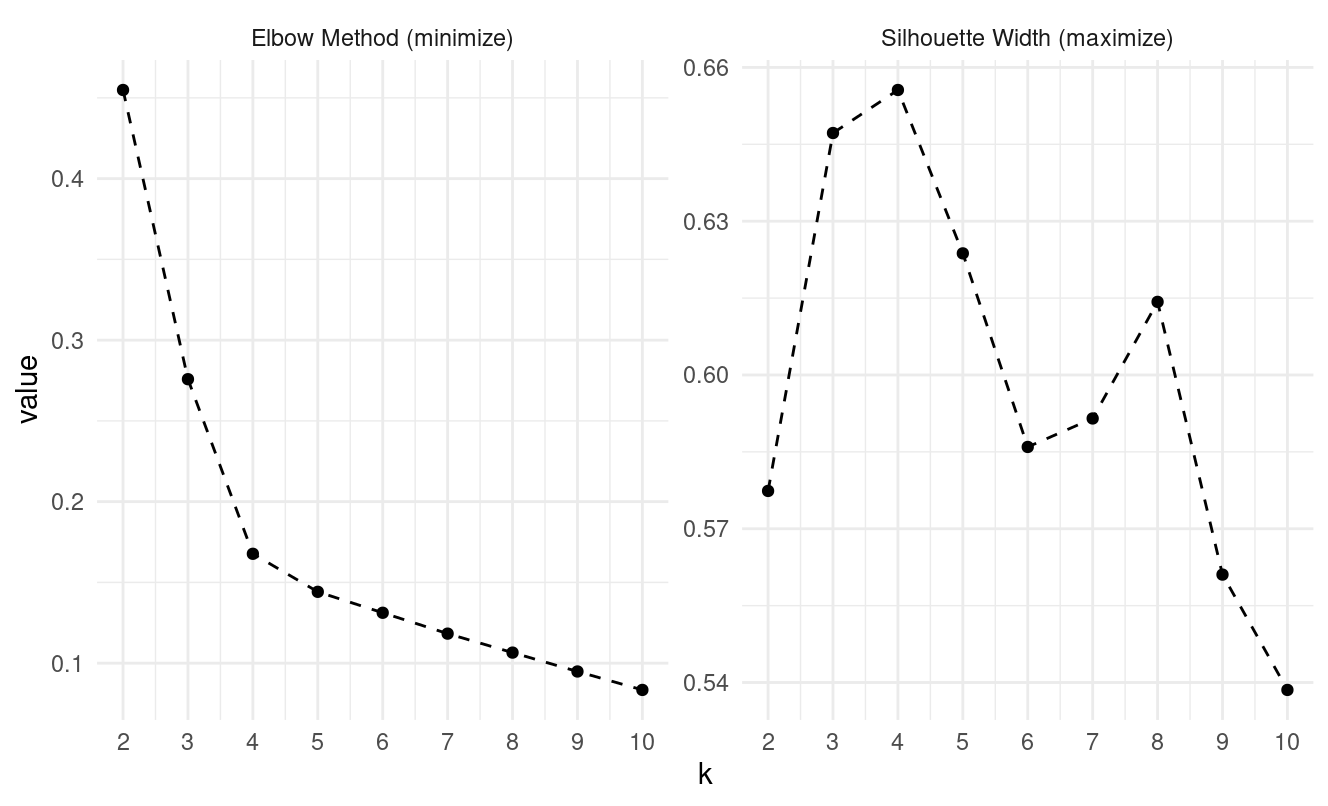
Key differences to implement:
- Use
pam(.x, k = .y)instead ofkmeans() - Extract clusters with
.y$clusteringinstead of.y$cluster - Replace
broom::glance(.x)with:r ~ tibble( tot.withinss = .x$objective[2], # Total cost from PAM k = .x$k )
Questions after running:
- What optimal k do the elbow and silhouette methods suggest?
Looking at the pam evaluation plots:
- Elbow method: the curve begins flattening at k = 4
- Silhouette: peaks at k = 4
Both methods suggest k = 4.
- How do k-medoids results compare to k-means?
- Both produce similar four well-defined clusters.
- k-medoids swaps some assignment boundaries slightly because medoids must be actual data points.
- The result is slightly more robust to outliers than k-means (in general).
- Overall, the cluster structure is almost identical — which is expected because the MCA coordinates form fairly spherical clusters.
Step 3: Apply to K-means++ (10 minutes)
Your Task: Modify the template for enhanced k-means with better initialization.
Key change:
set.seed(123)
mca_coords |>
select(dim_1:dim_2) |>
nest(data = everything()) |>
crossing(k = 2:10) |> # Start from k=2
mutate(
kmeans_result = map2(
data,
k,
~ kmeans(.x, centers = .y, algorithm = "Lloyd", nstart = 25)
),
glanced = map(kmeans_result, ~ broom::glance(.x)),
silhouette = map2_dbl(
data,
kmeans_result,
~ {
sil <- silhouette(.y$cluster, dist(.x))
mean(sil[, 3])
}
)
) |>
unnest(glanced) |>
select(k, tot.withinss, silhouette) |>
pivot_longer(c(tot.withinss, silhouette), names_to = "metric") |>
mutate(
metric = if_else(
metric == "tot.withinss",
"Elbow Method (minimize)",
"Silhouette Width (maximize)"
)
) |>
ggplot(aes(k, value)) +
facet_wrap(. ~ metric, scales = "free_y") +
geom_point() +
geom_line(linetype = "dashed") +
scale_x_continuous(breaks = 2:10) +
theme_minimal()
set.seed(123)
clusters <- kmeans(
mca_coords[, 1:2],
centers = 4,
algorithm = "Lloyd",
nstart = 25
)$cluster
mca_coords |>
mutate(cluster = as.factor(clusters)) |>
ggplot(aes(dim_1, dim_2, colour = cluster)) +
geom_point(size = 5) +
theme_minimal() +
ggsci::scale_colour_uchicago()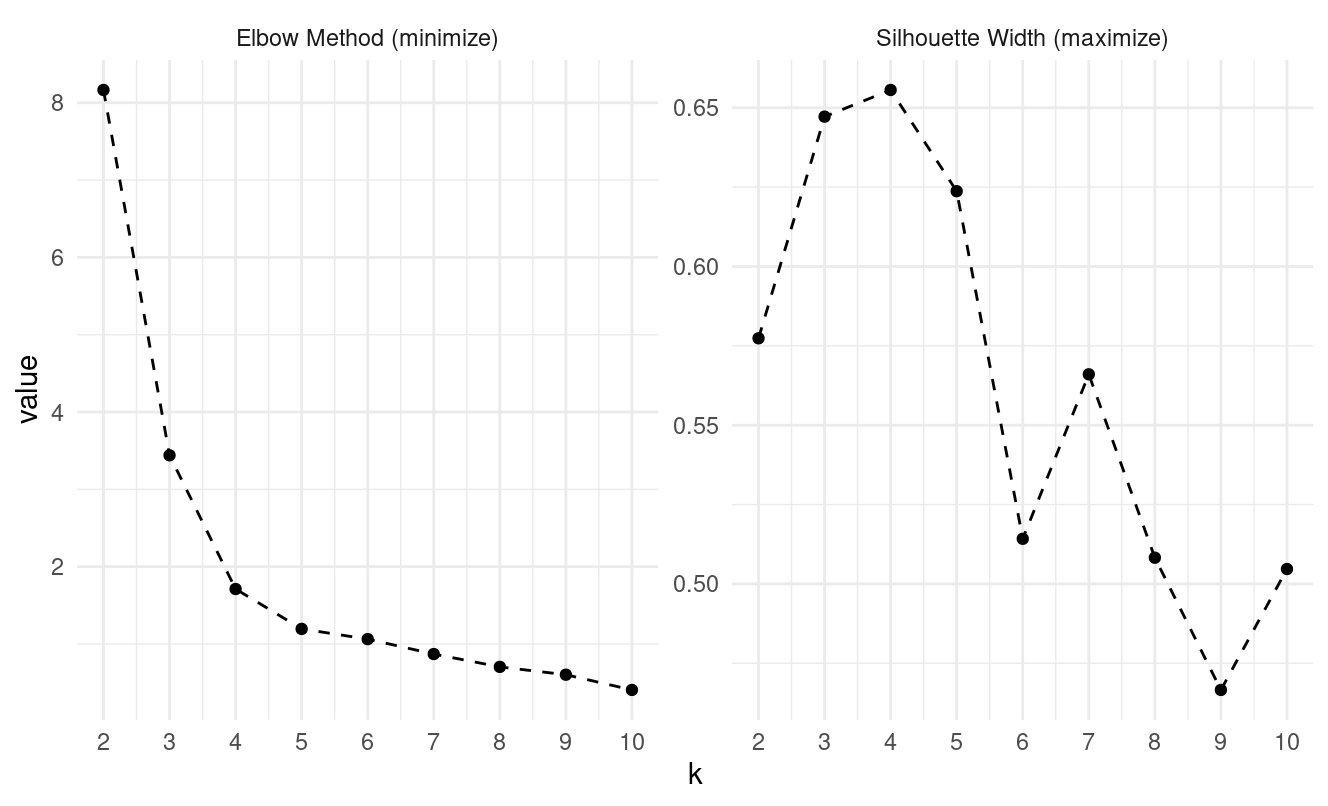
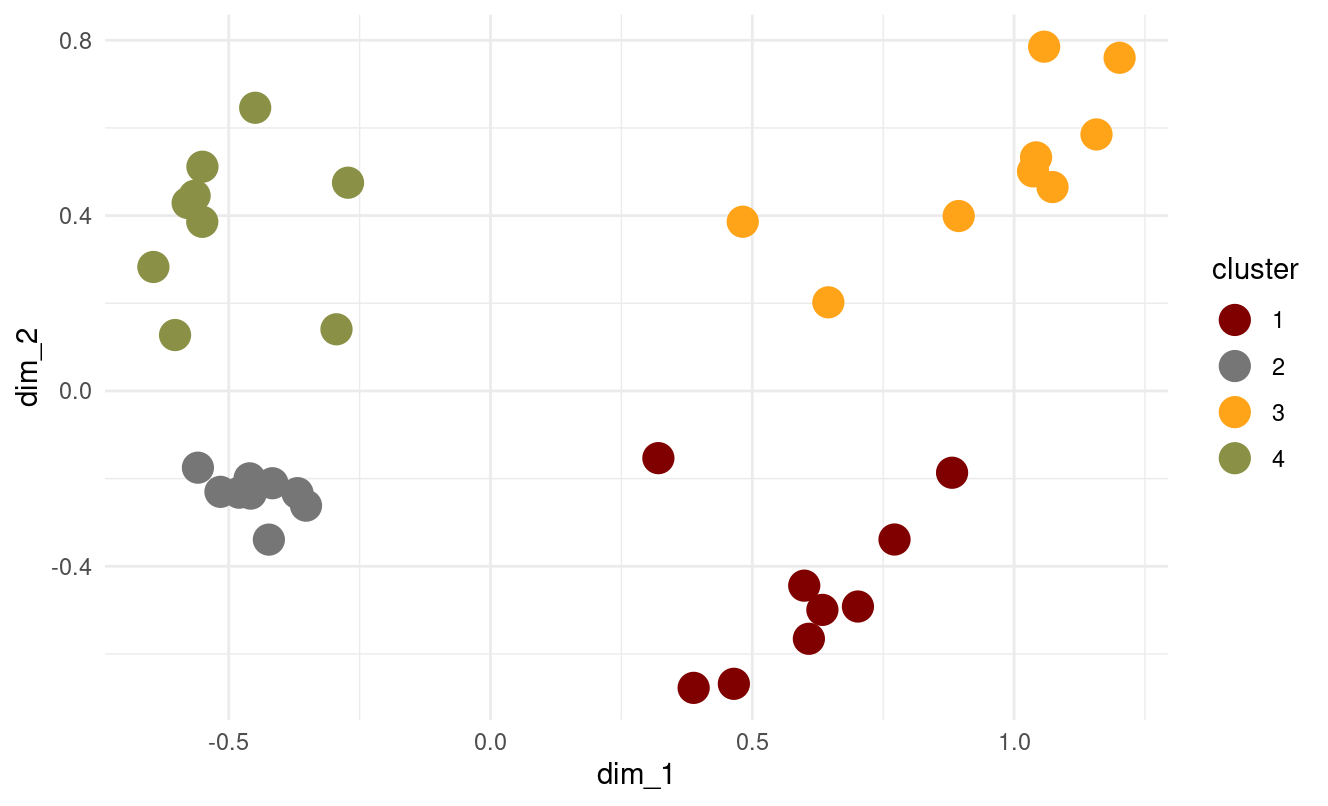
Questions:
- Do you notice differences in stability compared to basic k-means?
In this particular example, not exactly.
But, k-means++ generally:
- produces more consistent clusters across runs
- converges faster
- avoids poor local minima caused by bad center initialization
In our results, the k-means++ clustering matches the structure from basic k-means very closely.
- Does the optimal k suggestion change?
No — both elbow and silhouette curves again point to k = 4.
Step 4: Compare All Three Methods (10 minutes)
Create final clusterings using your chosen optimal k for all three methods:
# Compare all three with optimal k
set.seed(123)
optimal_k <- 4 # Use your chosen k
# k-means
kmeans_clusters <- kmeans(
mca_coords[, 1:2],
centers = optimal_k,
nstart = 25
)$cluster
# k-medoids
kmedoids_clusters <- pam(mca_coords[, 1:2], k = optimal_k)$clustering
# k-means++ (enhanced)
kmeans_plus_clusters <- kmeans(
mca_coords[, 1:2],
centers = optimal_k,
algorithm = "Lloyd",
iter.max = 1000,
nstart = 25
)$cluster
# Create comparison plots
p1 <- mca_coords |>
mutate(cluster = as.factor(kmeans_clusters)) |>
ggplot(aes(dim_1, dim_2, colour = cluster)) +
geom_point(size = 3) +
ggtitle("k-means") +
theme_minimal() +
ggsci::scale_colour_uchicago()
p2 <- mca_coords |>
mutate(cluster = as.factor(kmedoids_clusters)) |>
ggplot(aes(dim_1, dim_2, colour = cluster)) +
geom_point(size = 3) +
ggtitle("k-medoids") +
theme_minimal() +
ggsci::scale_colour_uchicago()
p3 <- mca_coords |>
mutate(cluster = as.factor(kmeans_plus_clusters)) |>
ggplot(aes(dim_1, dim_2, colour = cluster)) +
geom_point(size = 3) +
ggtitle("k-means++") +
theme_minimal() +
ggsci::scale_colour_uchicago()
p1 + p2 + p3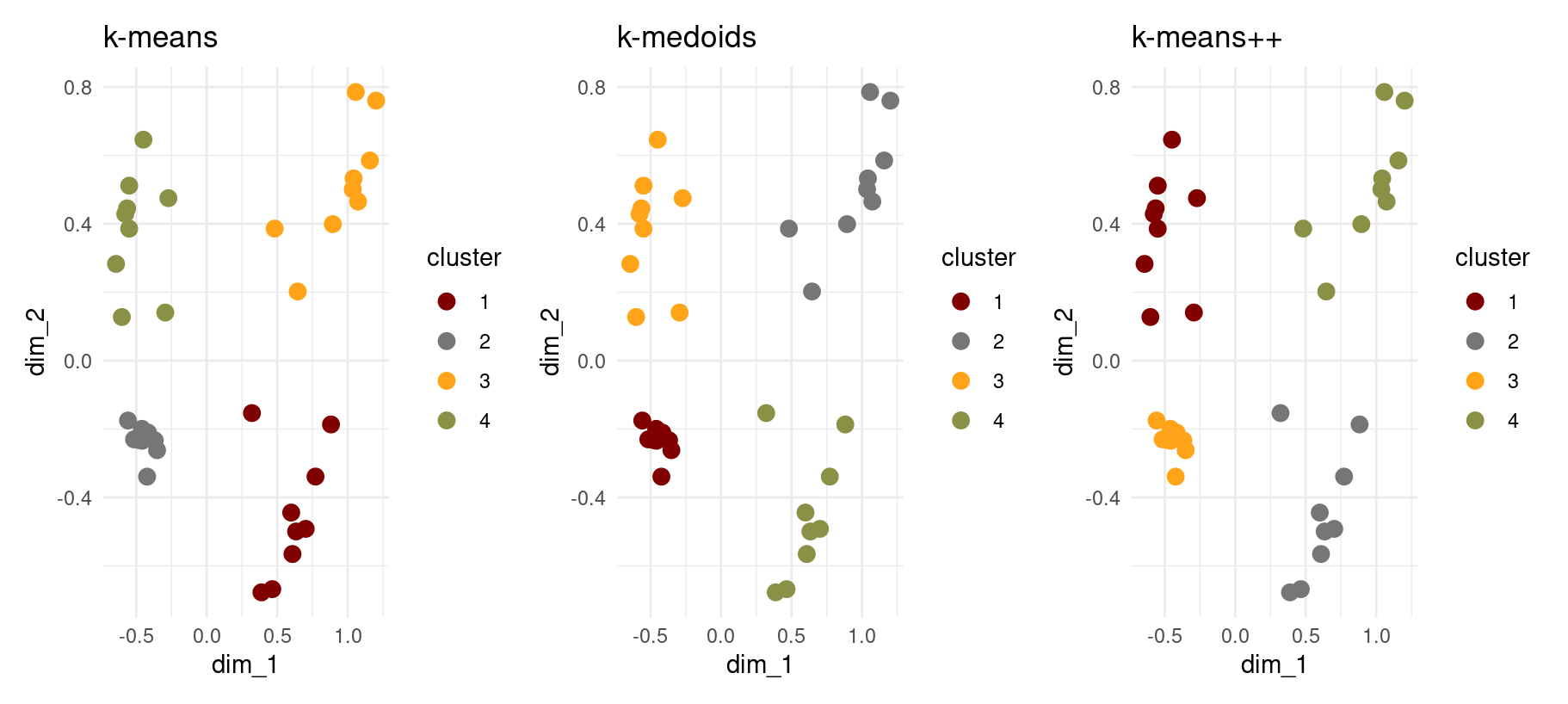
Discussion Questions:
- Which evaluation method (elbow vs silhouette) was most reliable across algorithms?
The silhouette method was more decisive. The elbow plot flattens gradually, but silhouette consistently shows:
- k-means peak at k = 4
- k-medoids peak at k = 4
- k-means++ peak at k = 4
So silhouette is more reliable for this dataset.
- Which clustering algorithm produced the best results for this dataset?
Based on the three side-by-side plots:
- k-means and k-medoids both produce clean, well-separated clusters.
- k-means++ improves center initialization but does not materially change the final clusters.
Best overall:
k-medoids Why? Because it handles distance geometry better, is robust to outliers, and still preserves the clean 4-cluster structure.
(though in this case, the final result wouldn’t really have changed no matter which algorithm we chose)
Also, bear in mind that k-medoids tends to be a bit more computationally expensive (and slower) than k-means. So, that should be something to consider too when evaluating cluster quality and choosing clustering algorithms.
- What are the key trade-offs between the three methods?
| Method | Strengths | Weaknesses |
|---|---|---|
| k-means | Simple, fast, clean clusters | Sensitive to initialization & outliers Assumes spherical clusters |
| k-means++ | Avoids poor starts, more stable | Still centroid-based and assumes spherical clusters |
| k-medoids | Robust to noise, works with any distance metric | Slower on larger datasets |
Part 3: DBSCAN - Density-Based Clustering (30 minutes)
DBSCAN is fundamentally different:
- No need to specify k
- Finds arbitrary shapes
- Identifies noise points
- Key parameters:
eps(neighborhood radius) andminPts(minimum points)
Task 4: Basic DBSCAN
# Start with reasonable parameters
db_result <- dbscan::dbscan(mca_coords[, 1:2], eps = 0.25, minPts = 5)
# Check results
cat("Clusters found:", max(db_result$cluster), "\n")
cat("Noise points:", sum(db_result$cluster == 0), "\n")
# Visualize
mca_coords_db <- mca_coords |>
mutate(cluster = as.factor(db_result$cluster))
clustered_points <- mca_coords_db |> filter(cluster != "0")
noise_points <- mca_coords_db |> filter(cluster == "0")
ggplot() +
geom_point(
data = clustered_points,
aes(dim_1, dim_2, color = cluster),
size = 4
) +
geom_point(
data = noise_points,
aes(dim_1, dim_2),
color = "red",
size = 5,
shape = 4 # shift the points
) +
geom_text(
data = noise_points,
aes(dim_1, dim_2, label = category),
color = "red",
size = 5
) +
labs(title = "DBSCAN Clustering", caption = "X marks indicate noise points") +
theme_minimal() +
ggsci::scale_colour_uchicago()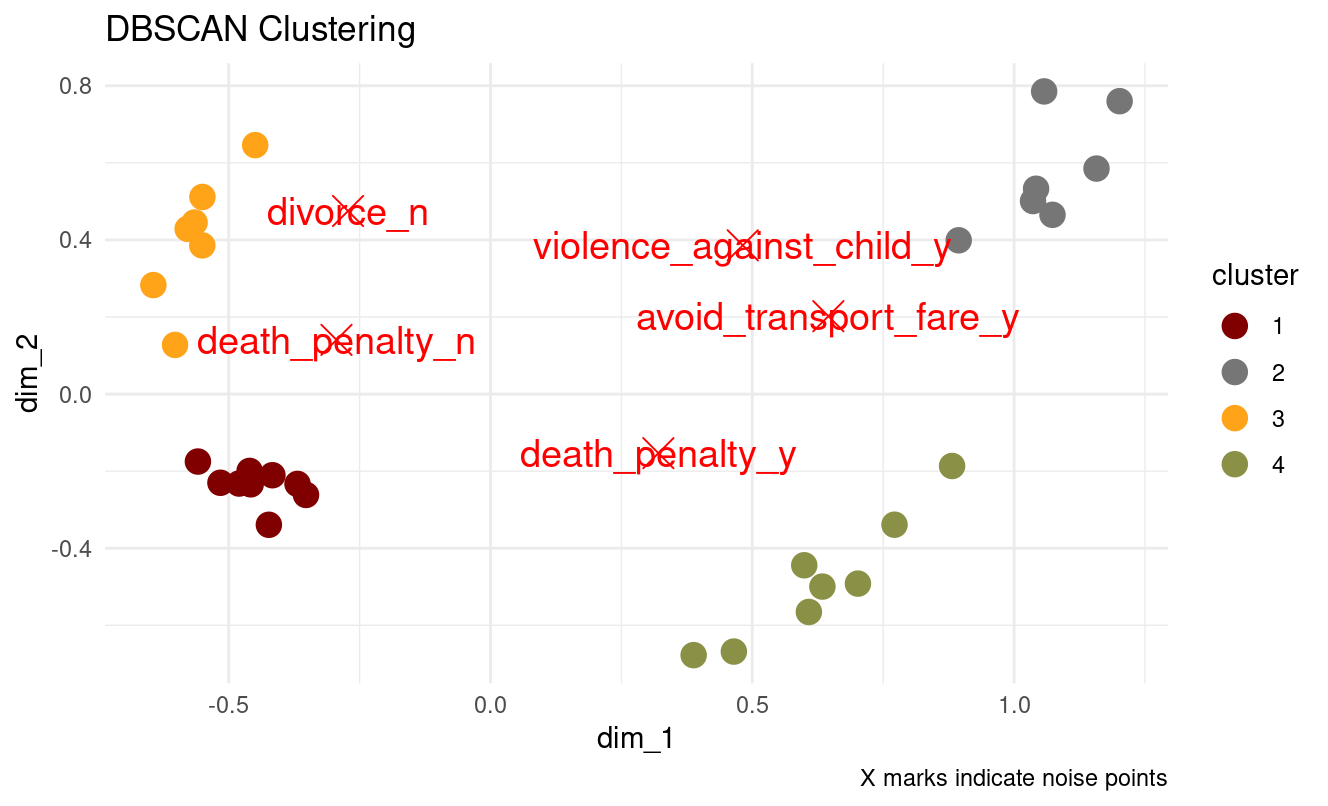
Task 5: Experiment with Epsilon
Try different eps values: c(0.1, 0.2, 0.3, 0.4, 0.5) and observe:
Key Questions:
- How does changing epsilon affect cluster formation?
- Low eps (0.1–0.2): very few points form clusters → most are noise
- Moderate eps (0.25–0.3): 3–4 meaningful clusters emerge
- High eps (0.4–0.5): clusters begin to merge incorrectly → eventually everything merges into one cluster
- What happens to noise points as epsilon changes?
- Small eps → many noise points
- Large eps → fewer noise points, because neighborhoods grow too large → noise disappears but clusters become meaningless
- Should all points belong to a cluster?
No. DBSCAN is designed to identify true noise/outliers. Noise points often carry important information.
- Which epsilon value seems most appropriate?
Our plot suggests eps ≈ 0.25–0.30, which should give:
- sensible clusters
- a reasonable number of noise points
- correct separation of four structure groups
Task 6: Final Comparison
Create side-by-side plots comparing your best k-means, k-medoids, and DBSCAN results.
Discussion Questions:
- Which method captures the structure of your data best?
- Centroid-based methods (k-means, k-means++, k-medoids) captured all 4 natural MCA clusters cleanly.
- DBSCAN, even with good eps, mislabels several boundary points as noise (though it might be worth checking those points).
For this dataset, k-medoids/k-means capture the structure best
- When would you choose DBSCAN over k-means/k-medoids?
- When clusters are irregularly shaped
- When dataset contains significant noise or outliers
- When cluster count should not be pre-specified
- What are the advantages of identifying noise points?
- It helps detect survey anomalies, rare categories, unusual respondents
- It prevents distortions in centroid-based algorithms
- It makes clusters more meaningful by removing edge cases
Summary Discussion
Reflect on:
- Which clustering method worked best for this dataset and why?
- How important was the choice of evaluation method?
- What are the key considerations when choosing clustering algorithms?
- When might you prefer density-based over centroid-based methods?
Key Takeaways
- Template approach: Similar code patterns work across clustering methods
- Evaluation matters: Elbow and silhouette can give different suggestions
- No universal best: Choice depends on data characteristics and goals
- DBSCAN advantages: Handles noise and arbitrary shapes, no k required
Homework Challenge
Apply these clustering methods to a dataset from your own field. Which method works best and why?
