🗓️ Week 05
From Randomness to Models

DS101 – Fundamentals of Data Science

Dr. Ghita Berrada

LSE Data Science Institute

2025-10-27

What we will cover today:

• From Randomness to Probability
• Describing Uncertainty: Probability Distributions
• From Association to Prediction
• When Correlation Misleads: Confounding
• Multiple Regression and Causal Thinking
• The Card & Krueger Natural Experiment (Card and Krueger 1993)
• When Models Mislead: Reinhart & Rogoff
• Looking Ahead: From Linear Models to Machine Learning

From Randomness to Probability

Where we left off last week

• We explored sampling and the Central Limit Theorem (CLT).
  
• The CLT told us that sample means fluctuate around the population mean in a roughly Normal way.
  
• But we have not yet asked:
  > what do we mean by “chance,” exactly?

For examples of how to apply the central limit theorem, see Chapter 6, section 6.2 of (Shafer and Zhang 2012) or this page or this page

Why talk about probability?

• Probability is how we quantify uncertainty.
  
• It lets us move from anecdotes (“probably rain tomorrow”) to numbers.
  
• Every data pattern involves some probability model underneath.

Example questions:

• What’s the chance of scoring above 15 on a test?
  
• What’s the probability that our sample average differs by more than 2 points from the truth?

What is a probability?

A probability is a number between 0 and 1 that measures the likelihood of an event.

Event	Probability	Example meaning
Impossible	0	Drawing 8 hearts in a row from a deck
Certain	1	Getting an even number from {2, 4, 6}
Intermediate	0 < p < 1	30 % chance of rain tomorrow

Three ways to interpret probability

Probability does not have a single universal meaning — it depends on how we think about uncertainty.

Interpretation	Core idea	Example
Classical	Probability is based on counting equally likely outcomes. All possibilities are known and symmetric.	Rolling a fair six-sided die: each face has 1 chance out of 6, so \(P(3)=\frac{1}{6}\).
Frequentist	Probability is the long-run relative frequency of an event after many repetitions of the same process.	Flip a fair coin 1 000 times → expect about 500 heads. The observed frequency (≈ 0.5) approaches the true probability as the number of trials increases.
Bayesian	Probability measures our degree of belief in a statement, which can be updated when new information arrives.	Before seeing data: you believe a vaccine is 90 % effective (\(P(\text{effective})=0.9\)). After new clinical results, you update that belief via Bayes’ rule.

Note

Classical → symmetry of outcomes
Frequentist → repetition and empirical frequencies
Bayesian → belief updating through evidence

Randomness in data

Randomness enters our analyses from several directions — not as “chaos,” but as variation we must model.

Source of randomness	What it means in practice	Example
Sampling variability	The specific individuals or observations we happen to select differ from one sample to another.	Two randomly chosen student groups produce slightly different average marks.
Measurement error	Our instruments or procedures introduce small fluctuations in values.	Teachers’ scoring differs by a few points even for similar work.
Behavioural or natural variability	Human and environmental processes are inherently variable.	Motivation, sleep, or stress levels vary daily — affecting performance.
Model uncertainty	Even the best model is an approximation; residual error remains.	Regression predictions never fit perfectly — the “ε” term captures what’s left unexplained.

Describing Uncertainty: Probability Distributions

The idea of a distribution

A probability distribution shows how likely different outcomes are.

• Uniform: all outcomes equally likely
  
• Normal: most near the centre
  
• Skewed: rare but extreme values in a long tail

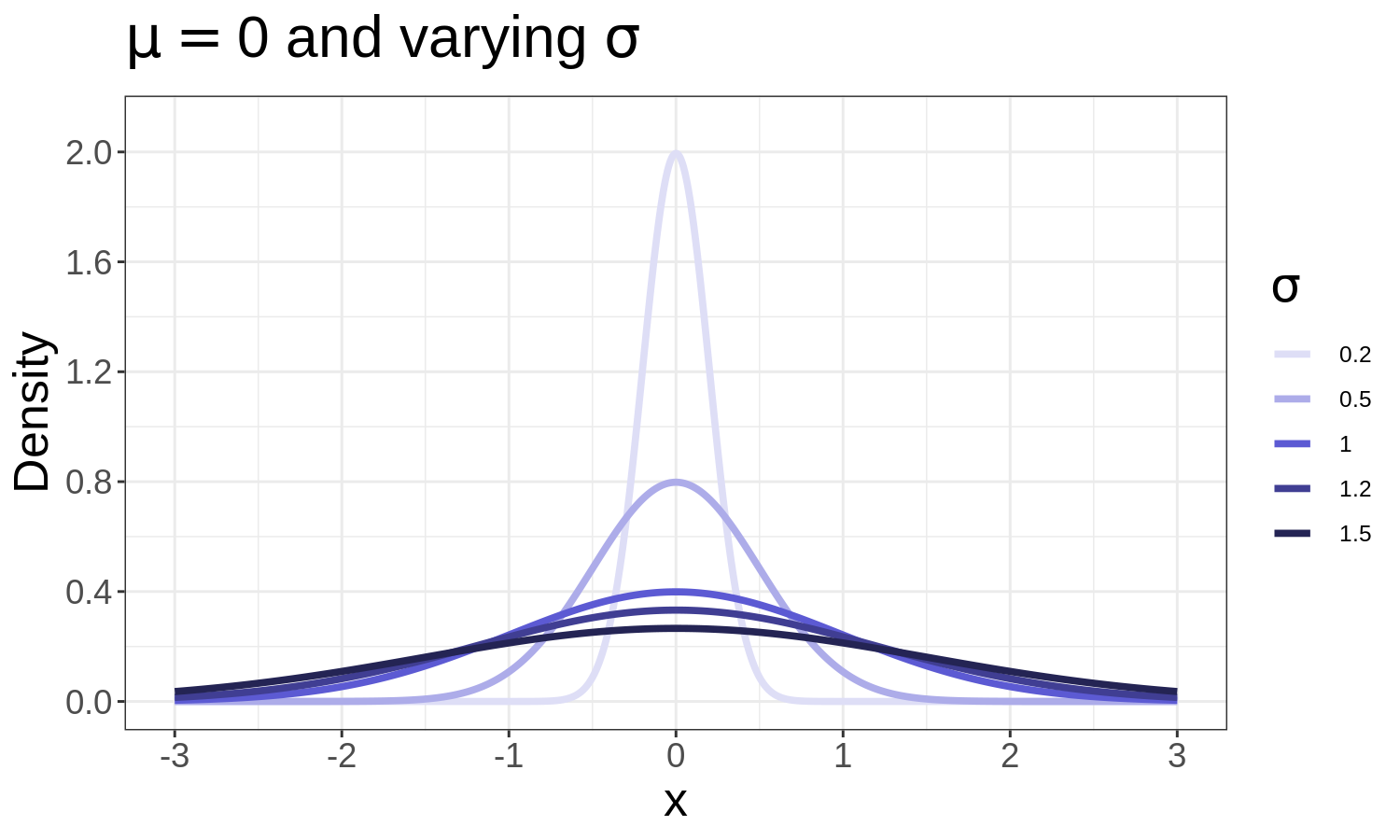
The Normal distribution

Formula:
\[ f(x; \mu, \sigma) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x-\mu)^2}{2\sigma^2}} \]

Where:

• \(x\): variable of interest
  
• \(\mu\): mean (centre)
  
• \(\sigma\): standard deviation (spread)

Examples: heights, exam marks, measurement errors.
≈ 68 % of values within ±1σ, 95 % within ±2σ.

For more on this topic, see Chapter 5 (sections 5.2 and 5.3) of (Shafer and Zhang 2012)

The Binomial distribution

Used for counting successes in n independent yes/no trials.

Formula:
\[ P(X = k) = \binom{n}{k} p^k (1-p)^{n-k} \]

Where:
- \(n\): number of trials
- \(k\): number of successes
- \(p\): probability of success in a single trial
- \(\binom{n}{k}\): number of possible ways to get k successes

Example: number of correct answers in 10 true/false questions.
As n grows and \(p≈0.5\), the shape becomes approximately Normal.

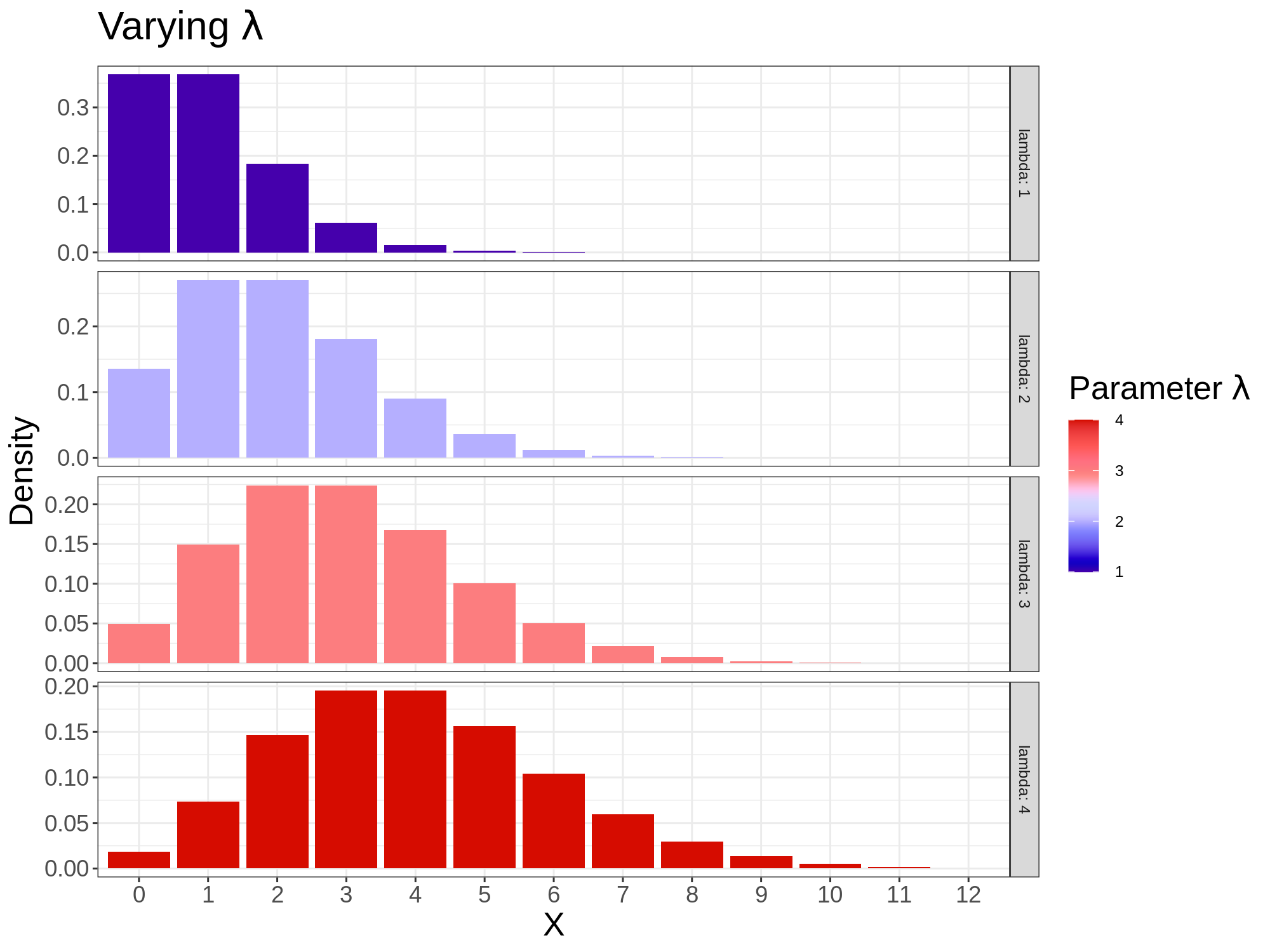
The Poisson distribution

Used for counts of rare events in a fixed interval.

Formula:
\[ P(X = k) = \frac{e^{-\lambda}\lambda^k}{k!} \]

Where:
- \(k\): number of occurrences
- \(\lambda\): average rate (mean number of events per interval)

Examples:
- Number of emails received per hour
- Accidents per day on a road

If \(\lambda\) is large → Poisson ≈ Normal.

For more on Poisson distribution, see this page.
For more on probability distributions,
see Chapter 4 of (Illowsky and Dean 2013).

The Exponential distribution

Models waiting times between independent events.

Formula:
\[ f(x; \lambda) = \lambda e^{-\lambda x}, \quad x \ge 0 \]

Where:
- \(x\): waiting time or duration
- \(\lambda\): rate (average number of events per unit time)

Example: minutes between bus arrivals.

Has the memoryless property i.e the probability of waiting another t minutes doesn’t depend on how long you’ve already waited.

The Gamma distribution

A flexible family for non-negative, skewed variables.
Includes the Exponential distribution as a special case (when shape = 1).

Formula:
\[ f(x; k,\lambda) = \frac{\lambda^k x^{k-1} e^{-\lambda x}}{\Gamma(k)}, \quad x \ge 0 \]

Where:

• \(x\): variable (non-negative quantity)
  
• \(k\): shape parameter (controls skewness)
  
• \(\lambda\): rate parameter (controls spread)
  
• \(\Gamma(k)\): the Gamma function (generalises factorial)

Applications: rainfall amounts, service times, insurance claims.

From distributions to modelling

Once we know how single variables behave, we can ask: > how do two variables vary together?

That’s the step from describing uncertainty → modelling relationships,
which leads us to linear regression.

From Association to Prediction

Why modelling?

• Probability helps us quantify randomness in one variable.
  
• Modelling helps us explain relationships between variables.
  
• Instead of asking “what is likely?”, we now ask “what changes with what?”

Association vs Prediction vs Causation

Question type	Example	What it tells us
Association	Do students who study more get higher marks?	They move together
Prediction	Can we predict a mark from study time?	Quantifies the relationship
Causation	Does studying more cause higher marks?	Requires experimental control

Regression sits between association and causation:
it models associations but doesn’t, by itself, prove cause and effect.

The Student Performance dataset

We’ll use a real dataset from Portuguese secondary schools (UCI repository).
Each row is a student, with variables such as:

Variable	Description	Type
studytime	weekly study time (1 = <2h, 4 = >10h)	ordinal
absences	number of missed classes	numeric
failures	past course failures	numeric
G3	final year grade in Mathematics (target variable)	numeric

Goal:
> Can we describe and predict students’ final grades from study time?

	studytime	absences	failures	G3
0	2	6	0	6
1	2	4	0	6
2	2	10	3	10
3	3	2	0	15
4	2	4	0	10

Visualising the relationship

Even with broad categories, students in higher studytime brackets tend to get higher grades.

What is univariate linear regression?

A linear model describes the average trend between two variables:

\[ \text{Grade} = \beta_0 + \beta_1(\text{Study Time}) + \varepsilon \]

Term	Interpretation
β₀	predicted grade when study time = 0
β₁	expected difference in average grade for each step up in studytime bracket
ε	random error (individual differences) or leftover part the model couldn’t explain

Interpreting the line

Example:

\[ \widehat{G3} = 9.33 + 0.53 \times \text{studytime} \]

• A student who studies less than 2 hours (studytime=1) → predicted grade ≈ 9.86
• A student who studies more than 10 hours (studytime=4) → predicted grade ≈ 11.45

Each for each step up in studytime bracket is associated with an average +0.53 points on the final grade.

What is a residual?

A residual is the difference between what the model predicts and what we actually observe:

\[ \text{Residual} = \text{Actual grade} - \text{Predicted grade} \]

• If residual = 0 → perfect prediction
• If positive → model underestimates
• If negative → model overestimates

How good is our model?

We can summarise its performance with:

Metric	Meaning	Interpretation
R² (R-squared)	Proportion of total variation in grades explained by the model	Higher is better (0–1)
MAE (Mean Absolute Error)	Average size of prediction errors (in grade points)	Lower is better
Residuals	The individual differences between predictions and actuals	Should scatter evenly around 0

Fitting the model

OLS Regression Results                            
==============================================================================
Dep. Variable:                     G3   R-squared:                       0.010
Model:                            OLS   Adj. R-squared:                  0.007
Method:                 Least Squares   F-statistic:                     3.797
Date:                Mon, 27 Oct 2025   Prob (F-statistic):             0.0521
Time:                        06:53:46   Log-Likelihood:                -1159.3
No. Observations:                 395   AIC:                             2323.
Df Residuals:                     393   BIC:                             2331.
Df Model:                           1                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const          9.3283      0.603     15.463      0.000       8.142      10.514
studytime      0.5340      0.274      1.949      0.052      -0.005       1.073
==============================================================================
Omnibus:                       33.290   Durbin-Watson:                   2.012
Prob(Omnibus):                  0.000   Jarque-Bera (JB):               39.231
Skew:                          -0.742   Prob(JB):                     3.03e-09
Kurtosis:                       3.429   Cond. No.                         6.83
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
R² = 0.010, MAE = 3.40

Typical results:

• β₁ ≈ +0.53 → each higher studytime bracket ≈ +0.53 grade point
• R² ≈ 0.010 → model explains 1% of grade variation: studytime alone doesn’t predict grades well, most of the variation in grades is due to other factors (e.g. prior performance, attendance, etc.).
• MAE ≈ 3.40 → predictions off by ~3.4 points on average i.e by 17% (since the scale is over 20). In practice, if someone’s actual grade is 9, the model will predict a grade between 5.6 and 12.4!

How confident are we in the coefficients’ estimates?

Confidence intervals for the coefficients of our univariate model

\[ G3 = \beta_0 + \beta_1(\text{studytime}) + \varepsilon \]

Coefficient	Estimate	95 % CI (lower – upper)	Interpretation
Intercept (β₀)	9.33 (avg.)	8.14 – 10.51	baseline grade for students in the lowest studytime bracket
Studytime (β₁)	0.53 (avg.)	-0.0048 – 1.072	each higher studytime bracket adds ≈ 0.53 points, with 95 % confidence that the true effect lies between -0.0048 and 1.072

How confident are we in the coefficients’ estimates?

What this means visually

• The dotted lines show how uncertain our estimate is.
• If we re-sampled data many times, most fitted lines would fall inside that band.
• Narrower bands → more certainty (less sampling variability).

What regression tells us

• There’s a slight positive association between study time and grades. It also shows that study time on its own is not enough as a predictor of grades.
• The line quantifies this relationship and allows simple prediction.
• But we cannot yet say why this relationship exists.

When Correlation Misleads: Confounding

A “productivity paradox”

Let’s imagine we collect this data:

Person	Cups of coffee/day	Productivity score
A	1	68
B	2	74
C	3	81
D	4	86
E	5	92

Looks like ⬆ coffee → ⬆ productivity.

Adding a third variable

What if productivity also depends on income?

People in higher income jobs may both drink more coffee and have more resources or autonomy — not because coffee itself boosts productivity.

What’s a confounder?

A confounder is a third variable that influences both the predictor and the outcome, creating a spurious association.

Variable	Relation to Coffee	Relation to Productivity	Effect
Income	High-income workers can afford more coffee	High-income jobs often allow more focus/resources	Creates false appearance of causation

The observed correlation disappears when we control for the confounder.

Why it matters

• Confounding is the reason “correlation ≠ causation.”
• Observational data alone often cannot distinguish between direct and indirect effects.
• To move from association to causation, we need controlled experiments or natural variation that mimics random assignment.

That’s exactly what economists David Card and Alan Krueger (Card and Krueger 1993) famously did.

Multiple Regression and Causal Thinking

From simple to multiple regression

A simple model has one predictor:

\[ G3 = \beta_0 + \beta_1(\text{studytime}) + \varepsilon \]

But grades depend on several factors, not only study time.

\[ G3 = \beta_0 + \beta_1(\text{studytime}) + \beta_2(\text{absences}) + \beta_3(\text{failures}) + \varepsilon \]

Term	Meaning
β₀	average grade for a student with all predictors = 0
β₁	expected change in grade per study time step, holding others fixed
β₂	change per extra absence
β₃	change per past failure
ε	individual noise or unmeasured factors

Fitting the model

OLS Regression Results                            
==============================================================================
Dep. Variable:                     G3   R-squared:                       0.135
Model:                            OLS   Adj. R-squared:                  0.128
Method:                 Least Squares   F-statistic:                     20.29
Date:                Mon, 27 Oct 2025   Prob (F-statistic):           3.07e-12
Time:                        07:16:09   Log-Likelihood:                -1132.6
No. Observations:                 395   AIC:                             2273.
Df Residuals:                     391   BIC:                             2289.
Df Model:                           3                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const         10.5172      0.622     16.903      0.000       9.294      11.741
studytime      0.2158      0.261      0.826      0.409      -0.298       0.729
absences       0.0341      0.027      1.260      0.208      -0.019       0.087
failures      -2.2015      0.295     -7.470      0.000      -2.781      -1.622
==============================================================================
Omnibus:                       30.800   Durbin-Watson:                   2.027
Prob(Omnibus):                  0.000   Jarque-Bera (JB):               35.771
Skew:                          -0.699   Prob(JB):                     1.71e-08
Kurtosis:                       3.468   Cond. No.                         30.9
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
R² = 0.135, MAE = 3.25

Typical summary:

Predictor	Coefficient	p-value	Interpretation
studytime	+0.22	0.409	more study → slightly higher grade
absences	0.03	0.0208	more absences → slightly higher grade!
failures	−2.2	< 0.001	each failure ≈ −2.2 points
constant	10.5	—	baseline grade

Visualising two predictors at once

Confidence intervals in multiple regression: How reliable are our coefficients?

Our model

\[ G3 = \beta_0 + \beta_1(\text{studytime}) + \beta_2(\text{absences}) + \beta_3(\text{failures}) + \varepsilon \]

95 % Confidence intervals

Coefficient	95 % CI (lower–upper)	Includes 0?	Interpretation
Intercept (β₀)	9.29 – 11.74	❌	baseline grade lies safely above 0 → well estimated
Studytime (β₁)	−0.30 – 0.73	✅	crosses 0 → effect not reliably positive once other factors included
Absences (β₂)	−0.02 – 0.09	✅	overlaps 0 → weak, possibly no clear effect
Failures (β₃)	−2.78 – −1.62	❌	clearly below 0 → strong negative association

Confidence intervals in multiple regression: How reliable are our coefficients?

Visual summary

• Once we add absences & failures, the “studytime effect” nearly disappears.

• This illustrates how adding confounders changes what seems significant.

• Only the failures bar lies entirely below 0 → we’re confident that past failures really reduce grades.

• The intervals for studytime and absences straddle 0 → their effects could be small or even zero after controlling for other variables.

Confidence intervals in multiple regression: How reliable are our coefficients?

What this means

• A confidence interval that includes 0 → model can’t rule out no effect.
• A confidence interval entirely above or below 0 → likely a real effect.
• Wider intervals mean greater uncertainty; narrower = more precise estimate.

Why multivariate regression matters

• Controls for confounders directly (e.g. absences).
• Lets us test several hypotheses in one equation.
• Still uses ordinary least squares (OLS)—we just add more columns.

Next we see how the same logic allows economists to study policy changes like the 1992 minimum-wage rise.

Tip

Ordinary Least Squares (OLS)

OLS finds the line that best fits the data by making the vertical gaps (errors) between the observed points and the line as small as possible on average.

In other words, it minimizes the sum of squared residuals — the total squared “miss” of the model.

What is Linear Regression

The generic supervised model:

\[ Y = \operatorname{f}(X) + \epsilon \]

is defined more explicitly as follows ➡️

Simple linear regression

\[ \begin{align} Y = \beta_0 +& \beta_1 X + \epsilon, \\ \\ \\ \end{align} \]

when we use a single predictor, \(X\).

Multiple linear regression

\[ \begin{align} Y = \beta_0 &+ \beta_1 X_1 + \beta_2 X_2 \\ &+ \dots \\ &+ \beta_p X_p + \epsilon \end{align} \]

when there are multiple predictors, \(X_p\).

Warning

• True regression functions are never linear!
• Although it may seem overly simplistic, linear regression is extremely useful both conceptually and practically.

The Card & Krueger Natural Experiment (Card and Krueger 1993)

The idea

New Jersey raised its minimum wage in 1992; neighbouring Pennsylvania did not.

How did employment in fast-food restaurants change?

This setup forms two groups (NJ = treatment, PA = control) and two time periods (before / after).

The regression model

\[ \text{Employment}_{it} = \beta_0 + \beta_1\text{Post}_t + \beta_2\text{NJ}_i + \beta_3(\text{Post}_t \times \text{NJ}_i) + \varepsilon_{it} \]

Symbol	Meaning	Interpretation
(i)	Restaurant	Each observation refers to a specific fast-food restaurant.
(t)	Time (before / after)	Indicates whether the observation is before or after New Jersey’s minimum-wage increase.
Postₜ	1 = after policy, 0 = before	Captures the time effect: how employment changed after the policy, for all restaurants.
NJᵢ	1 = New Jersey (treated), 0 = Pennsylvania (control)	Captures the group effect: how New Jersey differs from Pennsylvania before the policy.
Postₜ × NJᵢ	1 only for New Jersey after the policy	The interaction term — measures how New Jersey’s change after the policy compares to Pennsylvania’s.
β₃	Difference-in-Differences effect	The estimated impact of the minimum-wage increase on employment (the causal treatment effect).
εᵢₜ	Random error	Captures other unobserved factors affecting employment (e.g., local demand, management, random noise).

Evaluating the four cases

Group	Post	NJ	Predicted mean	Interpretation
PA before	0	0	\(\beta_0\)	Pennsylvania baseline (control, before)
PA after	1	0	\(\beta_0 + \beta_1\)	Time trend common to both states
NJ before	0	1	\(\beta_0 + \beta_2\)	Baseline NJ–PA difference
NJ after	1	1	\(\beta_0 + \beta_1 + \beta_2 + \beta_3\)	NJ change after the law

Subtracting rows:

\[ \text{Difference-in-Differences} = (\text{After–Before})_{NJ} - (\text{After–Before})_{PA} = \boxed{\beta_3}. \]

Now β₃ directly measures the employment impact of the policy.

Worked example

State	Before	After	Change
NJ	23.0	24.0	+1.0
PA	23.5	22.0	−1.5

\[ (\Delta NJ) - (\Delta PA) = 1.0 - ( -1.5 ) = 2.5 \]

→ about 2½ extra jobs per restaurant in New Jersey.

Seeing it graphically

Parallel lines would mean no effect; the gap shows the policy impact.

Using the real dataset

                            OLS Regression Results                            
==============================================================================
Dep. Variable:              EMP_TOTAL   R-squared:                       0.006
Model:                            OLS   Adj. R-squared:                  0.002
Method:                 Least Squares   F-statistic:                     1.636
Date:                Mon, 27 Oct 2025   Prob (F-statistic):              0.179
Time:                        08:19:38   Log-Likelihood:                -3134.9
No. Observations:                 801   AIC:                             6278.
Df Residuals:                     797   BIC:                             6297.
Df Model:                           3                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
Intercept     29.6923      1.376     21.584      0.000      26.992      32.393
post          -2.1728      1.952     -1.113      0.266      -6.004       1.659
state         -3.2859      1.531     -2.146      0.032      -6.292      -0.280
post:state     2.4867      2.173      1.144      0.253      -1.780       6.753
==============================================================================
Omnibus:                      154.337   Durbin-Watson:                   1.242
Prob(Omnibus):                  0.000   Jarque-Bera (JB):              400.203
Skew:                           0.992   Prob(JB):                     1.25e-87
Kurtosis:                       5.838   Cond. No.                         11.3
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

Model performance:
R² = 0.006
MAE = 9.34

Average employment by state and period:
state  period
0      after     27.519481
       before    29.692308
1      after     26.720312
       before    26.406442
Name: EMP_TOTAL, dtype: float64

Model performance

Metric	Value	Interpretation
R²	0.006	The model explains less than 1 % of the variation in restaurant employment — expected for a difference-in-differences (DiD) setup, which focuses on average group changes, not individual prediction.
MAE	9.3 employees	On average, predictions differ from actual employment by about 9 workers — roughly one-third of the typical restaurant’s staff size. This reflects wide variation in employment across restaurants rather than model failure.

Note

💡 Takeaway

• Low R² and high MAE are normal in policy evaluations like this one.
• The DiD model isn’t built to predict employment precisely — it estimates average treatment effects.
• The key result is the coefficient on the interaction term (β₃ ≈ +2.5): New Jersey’s employment rose by about 2½ jobs more than Pennsylvania’s after the minimum-wage increase.

Why this matters

• The regression is a standard OLS model — each β multiplies a column of numbers (0/1).
• The interaction term automatically computes the DiD contrast.
• Card & Krueger’s finding: raising the minimum wage did not reduce employment — if anything, jobs rose slightly in NJ.

When Models Mislead: Reinhart & Rogoff

The claim

Reinhart & Rogoff (2010) (Reinhart and Rogoff 2010):

“When debt > 90 % of GDP, growth collapses.”

Their spreadsheet error later overturned that conclusion.

What went wrong

• Excel range excluded 5 countries.
• Unusual averaging and data omissions.
• Corrected result: high-debt countries grew only slightly slower, not disastrously.

What went wrong

What went wrong

Debt/GDP range	Reinhart&Rogoff(2010) (Reinhart and Rogoff 2010)	Herndon (2013) (Herndon, Ash, and Pollin 2013)	What the plot shows
0–30 %	≈ 4 %	≈ 4 %	✅ identical high growth
30–60 %	≈ 2.8 %	≈ 3.1 %	✅ small gap, both around 3 %
60–90 %	≈ 2.9 %	≈ 3.2 %	✅ almost flat
> 90 %	−0.1 %	2.2 %	❌ large difference at high debt

Lesson: transparency and replication prevent huge policy mistakes.

Looking Ahead: From Linear Models to Machine Learning

Regression to prediction

All our models so far fit the pattern

\[ Y = f(X) + \varepsilon \]

where \(f\) is linear. Machine-learning methods simply let (f) be more flexible.

Ethics and responsibility

This week’s class: The Ofqual algorithm fiasco

How biased models can amplify inequality and why transparency, testing, and humility matter.

Important

All models are approximations. Some are useful—if we understand their limits.

References

Card, David, and Alan B Krueger. 1993. “Minimum Wages and Employment: A Case Study of the Fast Food Industry in New Jersey and Pennsylvania.” National Bureau of Economic Research Cambridge, Mass., USA. https://www.nber.org/papers/w4509.

Herndon, Thomas, Michael Ash, and Robert Pollin. 2013. “Does High Public Debt Consistently Stifle Economic Growth? A Critique of Reinhart and Rogoff.” Cambridge Journal of Economics 38 (2): 257–79. https://doi.org/10.1093/cje/bet075.

Illowsky, Barbara, and Susan L. Dean. 2013. Introductory Statistics. Houston, Texas: OpenStax College. https://openstax.org/details/books/introductory-statistics.

Reinhart, Carmen M., and Kenneth S. Rogoff. 2010. “Growth in a Time of Debt.” American Economic Review 100 (2): 573–78. https://doi.org/10.1257/aer.100.2.573.

Shafer, Douglas S., and Zhiyi Zhang. 2012. Introductory Statistics. Saylor Foundation. https://saylordotorg.github.io/text_introductory-statistics/.