🗓️ Week 03
Computational Thinking and Programming

DS101 – Fundamentals of Data Science

Dr. Ghita Berrada

LSE Data Science Institute

13 Oct 2025

Excel…

Mentimeter: What do you think of Excel?

Mentimeter: Excel mishaps

The Excel Problem

Excel is great for:

Quick data entry
Simple calculations
Basic visualization
Non-technical users

But dangerous for:

Data science workflows
Reproducible analysis
Large datasets
Collaborative projects

Let’s see why with some real examples…

Horror Story #1: Gene Names

Source: (Vincent 2020)

What happened:

Excel auto-converted gene names to dates
MARCH1 (short for “Membrane Associated Ring-CH-Type Finger 1”) → 1-Mar
SEPT2 (short for “Septin 2”)→ 2-Sep

The scale:

2016 study (Ziemann, Eren, and El-Osta 2016): ~20% of 3,597 genomics papers affected by Excel gene name conversion
2021 follow-up (Abeysooriya et al. 2021): Still 30.9% of 11,117 papers had errors
Problem persisted despite awareness!

The fix: 27 genes officially renamed (MARCH1 → MARCHF1)

Horror Story #2: COVID-19 Data Loss

Source: (Hern 2020)

The incident:

UK Public Health England used Excel as exchange format with local trusts
Hit the 65,536 row limit
Lost 16,000 COVID cases
Delayed contact tracing

Impact: Lives at risk

Horror Story #3: Economic Policy

Source: (“The Excel Depression” 2013)

Reinhart-Rogoff spreadsheet error:

Influential economics paper
Original results showed average real economic growth slows (a 0.1% decline) when a country’s debt rises to more than 90% of gross domestic product
Influenced austerity policies globally
But, Excel formula excluded 5 rows (i.e 5 countries: Australia, Austria, Belgium, Canada and Denmark)
Wrong conclusions about debt/GDP (when that error was corrected, the “0.1% decline” data became a 2.2% average increase in economic growth)

Lesson: Always check your formulas!

Horror Story #4: The London Whale

Source: (Kwak 2013)

Horror Story #4: The London Whale

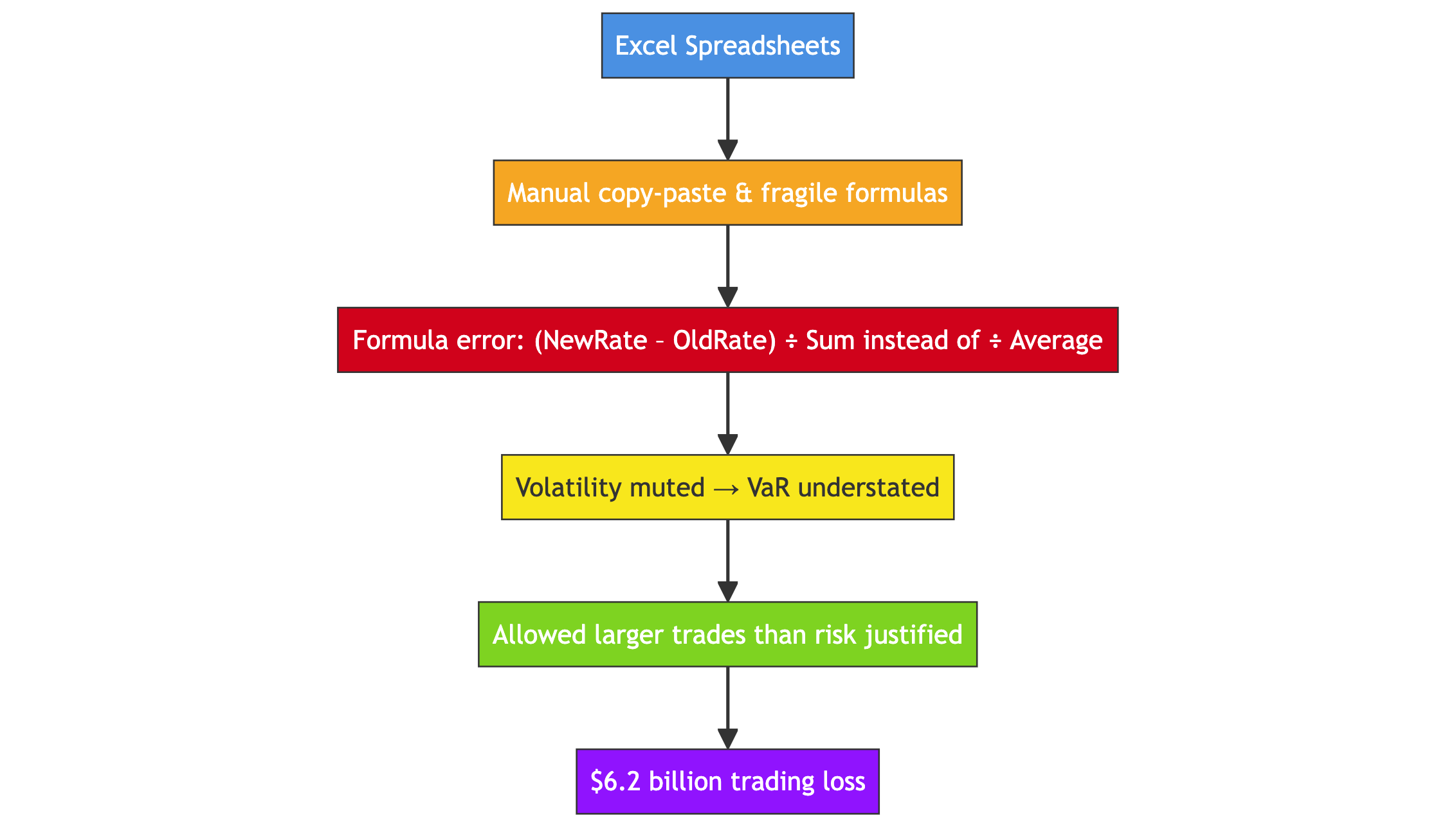
JP Morgan VaR Model (2012)

Built entirely in Excel
Manual copy-paste & fragile formulas
Formula error: divided by sum instead of average → VaR understated
Model review flagged issues but flaws never fixed
Resulted in $6.2 billion trading loss

Lesson:

Even sophisticated financial models fail on fragile, manually managed software. Critical calculations need robust, auditable systems.

Horror Story #5: Microsoft and Finance

Source: (Beales 2013)

A pattern of Excel-related failures:

2007 CPDOs (i.e Constant proportion debt obligations): Moody’s coding error inflated structured finance ratings (pre-crisis)
2012 London Whale: JPMorgan’s Excel-based risk model failures ($6.2B loss)
2013 Reinhart-Rogoff: Spreadsheet error undermined influential austerity research

The pattern: Office tools used as substitutes for proper systems and critical thinking

The Excel Takeaway

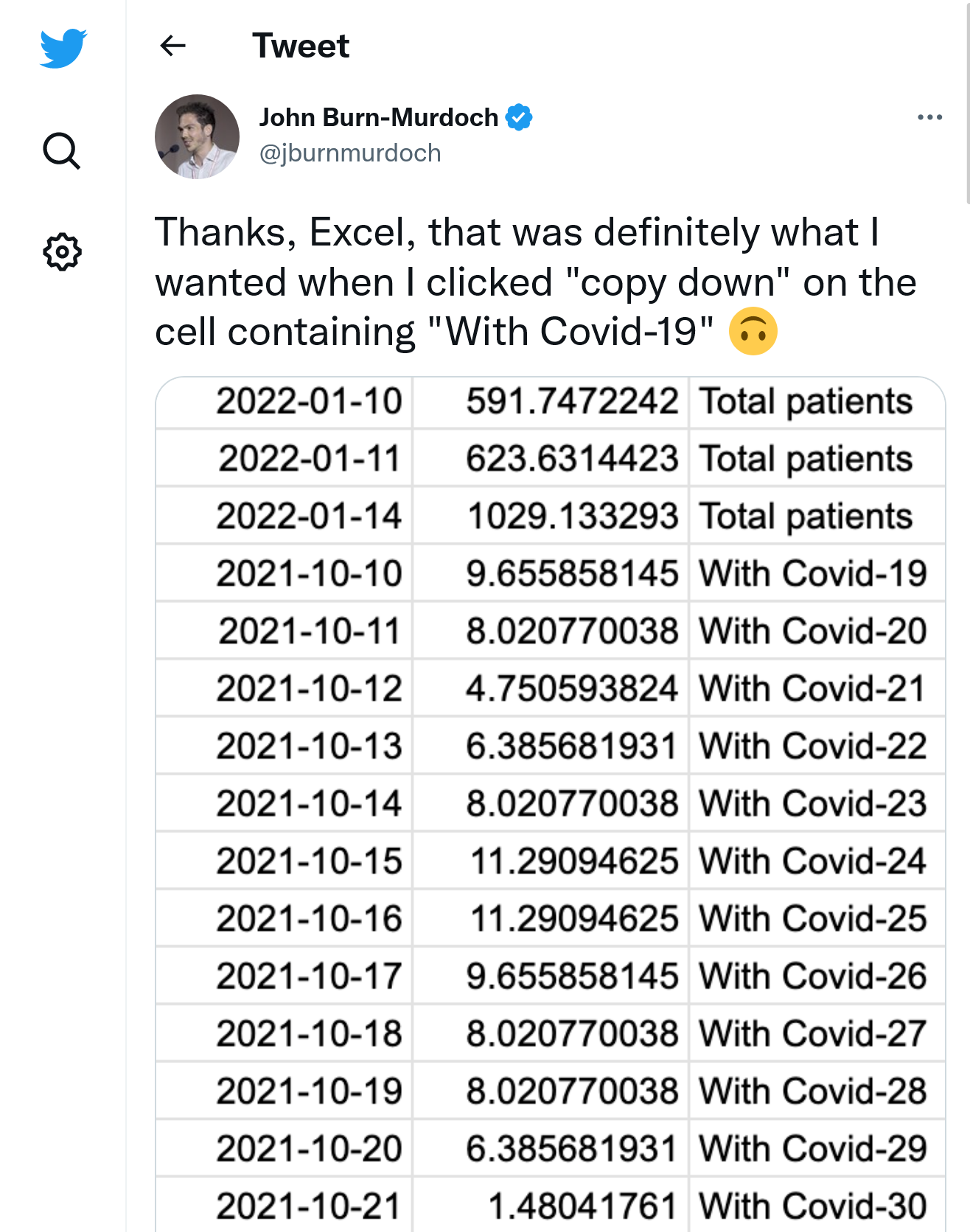
Excel is NOT for:

Serious data science
Reproducible analysis
Large-scale data processing
Production systems

Excel IS fine for:

Quick data exploration
Small personal datasets
Initial data entry
Simple calculations

Just know its limitations!

Excel wrap-up Mentimeter 💭

What do these stories have in common?

Human error 🧍‍♀️
Hidden assumptions
Manual, fragile processes
Tools used beyond their limits

“Excel doesn’t make mistakes. People do.”

It’s not about Excel…

These stories aren’t really about spreadsheets.
They’re about thinking — or rather, the lack of computational thinking.

From Chaos to Clarity

Spreadsheet World	Computational Thinking
🧍‍♀️ Manual formulas	🤖 Explicit procedures
❌ Hidden logic	✅ Transparent logic
😬 Fragile systems	💪 Reproducible steps
🌀 Chaos	🧩 Clarity

Computational Thinking

Mentimeter quiz

What is computational thinking? 🧠

A mindset for solving problems so precisely that a computer could follow your logic — even if it’s terrible coffee-fuelled logic ☕💻

More formally, it involves:

1️⃣ Designing computations that get computers to do jobs for us
2️⃣ Explaining and interpreting the world as a complex information process

Two Aspects of Computational Thinking

1️⃣ Designing computations (thinking like a computer)

Input: numbers, symbols, lists
Output: a solution
Computation: deterministic calculations & symbolic manipulation
Example: sorting a list, calculating shortest paths

2️⃣ Explaining and interpreting the world (modeling complexity)

Example: Schelling’s segregation model 🏘️ (McCown 2014)

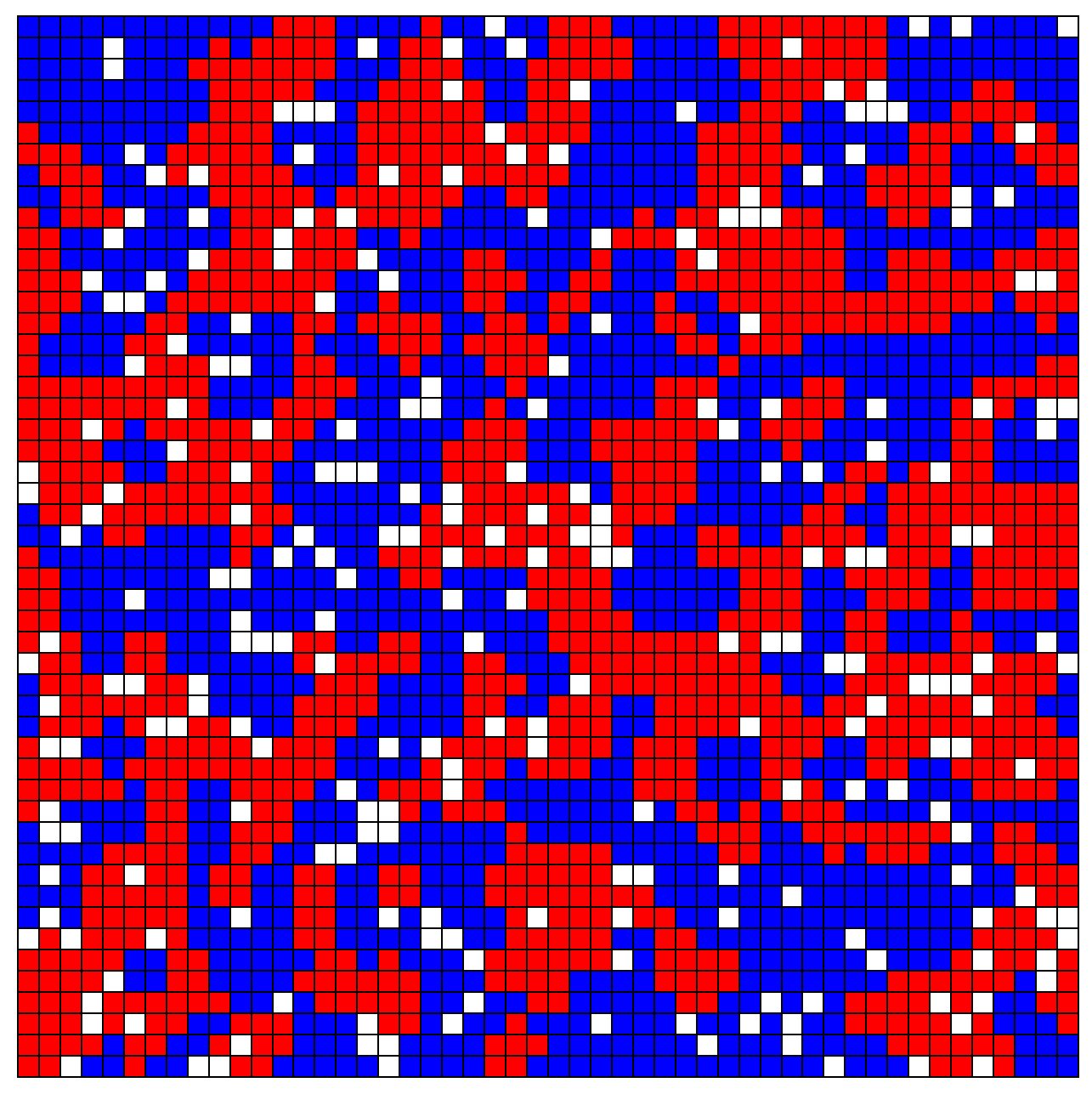
💬 Discussion Prompt:
- “What patterns do you think emerge if residents move when unhappy?”

Schelling Model – How it works

Input: grid of neighbouring households (two colors to distinguish type), tolerance threshold (e.g 30% of neighbours of different type)

Output: reordered grid

Each resident checks neighbors
If below tolerance threshold → move to nearest empty spot that satisfies preference
Repeat until all residents are “happy”

💬 Observation:
- Mild individual preferences → strong segregation patterns
- No one intended overall segregation → emergent behavior

Schelling Model – Computational Thinking Takeaway

Computers allow many iterations quickly
Helps explain real-world social patterns
This is an algorithm: rules → step-by-step, deterministic computation

“Next, we’ll focus on designing precise rules — algorithms — to solve tasks.”

Try It Yourself: Making Tea ☕

Imagine a robot has never seen tea.

Task: Write the first three instructions to make a cup of tea.
💬 Discuss at your table: what’s tricky about giving precise instructions?

Tea Algorithm ☕

One possible precise algorithm:

Fill kettle
Boil water
Put tea bag in cup
Pour water
Wait 3 minutes
Remove tea bag
Enjoy ☕

💬 Step-by-step, unambiguous, finite, feasible — now let’s formalize algorithm properties.

What is an algorithm? 📊

Definition:
- A recipe for solving a problem in a finite, step-by-step, unambiguous way

Properties:

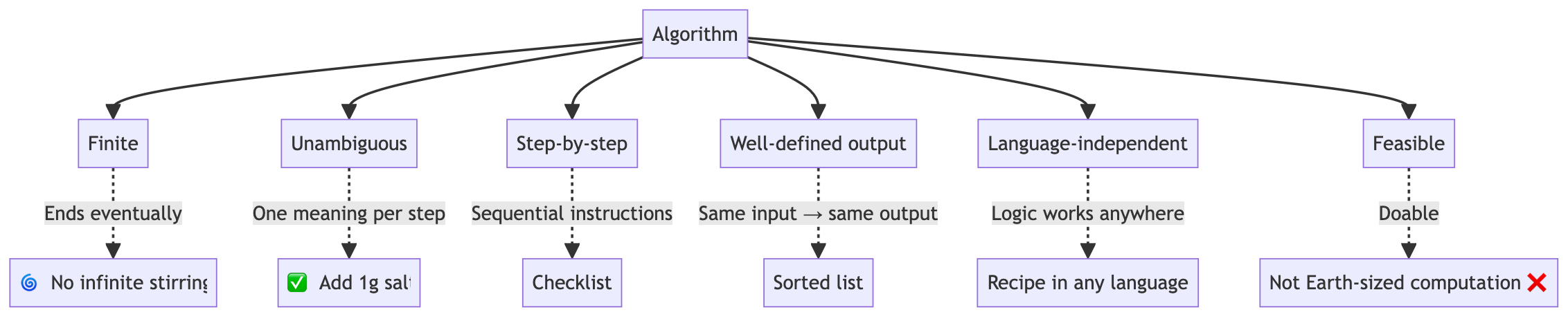
Sorting…

Input:

[10, 20, 42, 29, 50]
Output:

[10, 20, 29, 42, 50]
Computation:

How would you solve it❓

🎯 Action Point

Group up with the people of your respective tables and try to come up with a recipe that solves the problem, regardless of the list size.
Test that your recipe works for the following list:

[237, 153, 311, 33, 854, 212, 368, 42, 892, 755]

Time for a break 🍵

After the break:

Other algorithm examples

Time to look at another example of algorithm

Scenario: Campus walk from Marshall Building to other locations

Graph (distances in meters):

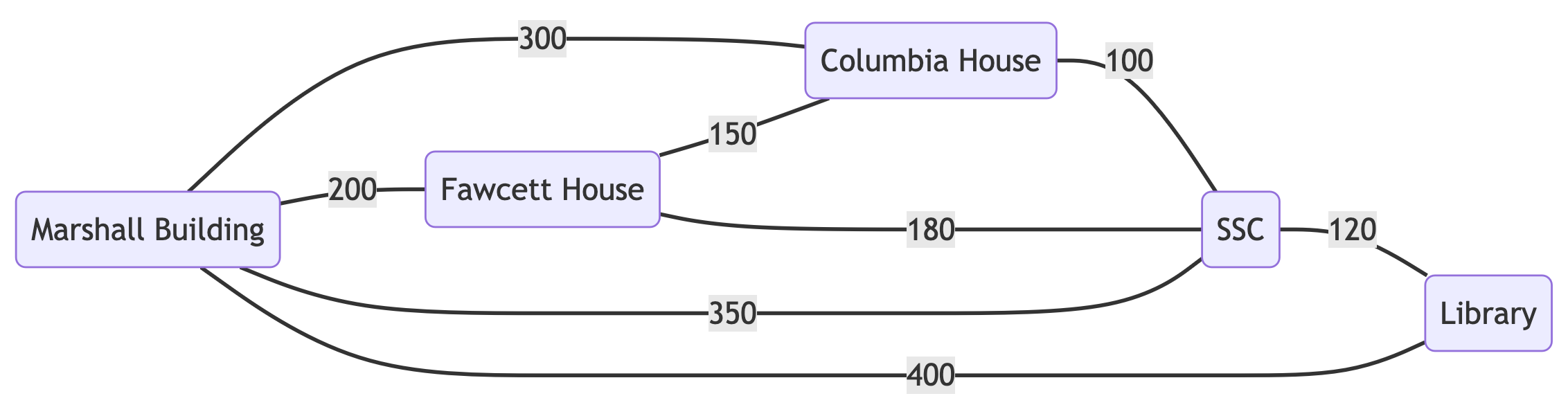
Discovery:

Could you try and find the shortest path from Marshall → all other nodes?

Dijkstra’s Algorithm – Step by Step Solution

Step 0 – Initialization:

MAR=0, others=∞
Previous = undefined
Unvisited={MAR,FAW,COL,SSC,LRB}

	MAR	FAW	COL	SSC	LRB
Distance	0	$\infty$	$\infty$	$\infty$	$\infty$

Dijkstra’s Algorithm – Step by Step Solution

Step 1 – Current node = MAR

Update neighbors:
- FAW: 0+200=200 → FAW=200, prev=MAR
- COL: 0+300=300 → COL=300, prev=MAR
- SSC: 0+350=350 → SSC=350, prev=MAR
- LRB: 0+400=400 → LRB=400, prev=MAR
Mark MAR visited

	MAR	FAW	COL	SSC	LRB
Distance	0	200	300	350	400

Dijkstra’s Algorithm – Step by Step Solution

Step 2 – Current node = FAW (200)

Neighbors: COL, SSC
COL: via FAW 200+150=350 > 300 → no update
SSC: via FAW 200+180=380 > 350 → no update
Mark FAW visited

	MAR	FAW	COL	SSC	LRB
Distance	0	200	300	350	400

Dijkstra’s Algorithm – Step by Step Solution

Step 3 – Current node = COL (300)

Neighbor: SSC
SSC: via COL 300+100=400 > 350 → no update
Mark COL visited

	MAR	FAW	COL	SSC	LRB
Distance	0	200	300	350	400

Dijkstra’s Algorithm – Step by Step Solution

Step 4 – Current node = SSC (350)

Neighbor: LRB
LRB: via SSC 350+120=470 > 400 → no update
Mark SSC visited

	MAR	FAW	COL	SSC	LRB
Distance	0	200	300	350	400

Dijkstra’s Algorithm – Step by Step Solution

Step 5 – Current node = LRB (400)

Neighbors: none unvisited
Mark LRB visited → Done

	MAR	FAW	COL	SSC	LRB
Distance	0	200	300	350	400

Dijkstra’s Algorithm – Step by Step Solution

Final shortest distances & paths:

Node	Distance	Path
MAR	0	MAR
FAW	200	MAR → FAW
COL	300	MAR → COL
SSC	350	MAR → SSC
LRB	400	MAR → LRB

Dijkstra’s algorithm in words

Step 1: Mark the source node with a current distance of 0 and the rest with infinity
Step 2: Set the non-visited node with the smallest current distance, as the current node, let’s say c (initially c is set to the source node).
Step 3: For each neighbour N of the current node c: add the current distance of c with the weight of the edge c-N. If it is smaller than the current distance of N, set it as the new current distance of N.
Step 4: Mark c as visited.
Step 5: Go to Step 2 if there are any unvisited nodes.

Use cases for shortest path algorithms (and Dijkstra algorithm)

find optimal directions between locations (e.g Google Maps-see here for a further explanation)/GPS Navigation: considering real-traffic conditions, calculate the shortest path between a source and destination in navigation systems
determine the shortest path between network nodes, helping in efficiently routing data packets (used in computer networks but also telephone networks)
recommendation systems: find the most relevant and shortest path between items or users (e.g movie recommendations, recommendations of items to buy)
social networks: suggest a list of friends that a user may know

For other applications, see also Schulz, Wagner, and Weihe (2000), Rosyidi et al. (2014) and Ahdan and Setiawansyah (2021)

Time for some voting! 🗳️

Scenario: Let’s votes for favorite café/tea shop!

Voters: Vansh, Unai, Manuela, Ria, Luka, Ziad, Zayd
Options: Pürcha, Garrick, Blank Street Café

Here are the voters’ preferences?

Preferences:

Student	Rank 1	Rank 2	Rank 3
Vansh	Pürcha	Garrick	Blank Street Café
Unai	Blank Street Café	Pürcha	Garrick
Manuela	Garrick	Pürcha	Blank Street Café
Ria	Garrick	Blank Street Café	Pürcha
Luka	Pürcha	Garrick	Blank Street Café

Discovery: How would you go about the vote?

Voting: a breakdown

Majority Vote

Count first-place votes:
- Pürcha: Vansh + Luka = 2
- Garrick: Manuela + Ria = 2
- Blank Street Café: Unai = 1
No majority (>50%) → need tie-break rules or runoff
Observation: Borda count can break ties where majority fails

Borda Count

Assign points to each rank: 1st place = 3 pts, 2nd = 2 pts, 3rd = 1 pt
Sum points:
- Pürcha: Vansh 3 + Unai 1 + Manuela 2 + Ria 1 + Luka 3 = 10
- Garrick: Vansh 2 + Unai 1 + Manuela 3 + Ria 3 + Luka 2 = 11
- Blank Street Café: Vansh 1 + Unai 3 + Manuela 1 + Ria 2 + Luka 1 = 8

✅ Winner (Borda): Garrick (11 pts)

Voting algorithms in words

Borda count

Assign points to ranks
Sum points per option
Option with highest total wins

Majority voting

Count first-choice votes
Option with >50% wins
If none, apply tie-break/runoff

Time for assigning tasks!

Suppose you had the following scenario:

Students: Vansh, Unai, Manuela Tasks: Prepare slides, Book meeting room room, Bring snacks

Original costs (time in minutes):

	Slides	Room	Snacks
Vansh	10	15	9
Unai	9	18	5
Manuela	6	14	3

How would you go about assigning the tasks?

How does the Hungarian algorithm work?

Step 1 — Subtract the minimum from every element of each row

	Slides	Room	Snacks
Vansh	10	15	9
Unai	9	18	5
Manuela	6	14	3

$->$

	Slides	Room
Vansh	1	6
Unai	4	13
Manuela	3	11

How does the Hungarian algorithm work?

Step 2 — Subtract the minimum of each column

	Slides	Room
Vansh	1	6
Unai	4	13
Manuela	3	11

$->$

	Slides	Room
Vansh	0	0
Unai	3	7
Manuela	2	5

How does the Hungarian algorithm work?

Step 3 — Cross 0s with the minimum number of lines needed

❌

	Slides	Room
Vansh	0	0
Unai	3	7
Manuela	2	5

✅

	Slides	Room
Vansh	0	0
Unai	3	7
Manuela	2	5

If the number of lines is < $n$, the number of rows and columns in the matrix, reduce the matrix again (i.e step 4). In our example, we have 2 lines, but we have a 3x3 matrix, so we’ll reduce again. If we didn’t have this case, we’d directly jump to step 5.

How does the Hungarian algorithm work?

Step 4 — Find the smallest entry not covered by any line, and subtract this entry from the entire non-crossed matrix (and add it to the elements crossed twice).

	Slides	Room
Vansh	0	0
Unai	3	7
Manuela	2	5

$->$

	Slides	Room	Snacks
Vansh	0	0	2
Unai	1	5	0
Manuela	0	3	0

then go back to step 3: cross the 0s!

	Slides	Room	Snacks
Vansh	0	0	2
Unai	1	5	0
Manuela	0	3	0

This time, we have three lines so we can go to step 5.

How does the Hungarian algorithm work?

Step 5 — Assign Tasks and Students starting with the line with only one zero!

	Slides	Room	Snacks
Vansh	0	0	2
Unai	1	5	0
Manuela	0	3	0

We start with the line with only one zero (there’s only one!) and assign its job to the corresponding student i.e Snacks to Unai. We then cross its row and column to make it unavailable.
The row that then contains a single zero corresponds to Manuela for Slides: so Slides is assigned to Manuela. Again, we cross the corresponding row and column.
We’re left with Room for Vansh. And so, we have our optimal assignment!

Hungarian algorithm Summary

Row Reduction: Subtract row minimums
Column Reduction: Subtract column minimums
Cover Zeros: Use minimum lines to cover all zeros
Check: If lines = n, done; else continue to step 5
Create Zeros: Adjust matrix using smallest uncovered value
Repeat: Steps 3-5 until optimal
Assign: Match zeros to create assignments

Some resources to go further

Video about the concept of algorithms explained in various and increasing levels of complexity: see here
Some basic details about how search engines work: see here

References

Abeysooriya, Mandhri, Megan Soria, Mary Sravya Kasu, and Mark Ziemann. 2021. “Gene Name Errors: Lessons Not Learned.” PLoS Computational Biology 17 (7): e1008984.

Ahdan, Syaiful, and Setiawansyah Setiawansyah. 2021. “Android-Based Geolocation Technology on a Blood Donation System (BDS) Using the Dijkstra Algorithm.” IJAIT (International Journal of Applied Information Technology), 1–15.

Bailey, David H., and Jonathan Borwein (Jon). 2013. “The Reinhart-Rogoff Error – or How Not to Excel at Economics. The Conversation.” April 22, 2013. http://theconversation.com/the-reinhart-rogoff-error-or-how-not-to-excel-at-economics-13646.

Beales, Richard. 2013. “Blame Microsoft.” New York Times (Online). 2013. https://www.proquest.com/blogs-podcasts-websites/blame-microsoft/docview/2215333604/se-2.

Denning, Peter J., and Matti Tedre. 2019. Computational Thinking. The MIT Press Essential Knowledge Series. Cambridge, Massachusetts: The MIT Press.

HackerEarth. 2023. “Bubble Sort Visualize Sorting Algorithms.” HackerEarth. https://www.hackerearth.com/practice/algorithms/sorting/bubble-sort/visualize/.

Hern, Alex. 2020. “Covid: How Excel May Have Caused Loss of 16,000 Test Results in England.” The Guardian. https://www.theguardian.com/politics/2020/oct/05/how-excel-may-have-caused-loss-of-16000-covid-tests-in-england.

Kwak, James. 2013. “The Importance of Excel.” "The Baseline Scenario" Blog, February. https://baselinescenario.com/2013/02/09/the-importance-of-excel/.

McCown, Frank. 2014. “Schelling’s Model of Segregation.” Schelling’s Model of Segregation. http://nifty.stanford.edu/2014/mccown-schelling-model-segregation/.

Rosyidi, Lukman, Hening Pram Pradityo, Dedi Gunawan, and Riri Fitri Sari. 2014. “Timebase Dynamic Weight for Dijkstra Algorithm Implementation in Route Planning Software.” In 2014 International Conference on Intelligent Green Building and Smart Grid (IGBSG), 1–4. IEEE.

Schulz, Frank, Dorothea Wagner, and Karsten Weihe. 2000. “Dijkstra’s Algorithm on-Line: An Empirical Case Study from Public Railroad Transport.” Journal of Experimental Algorithmics (JEA) 5: 12–es.

“The Excel Depression.” 2013. New York Times (Online). https://gate3.library.lse.ac.uk/login?url=https://www.proquest.com/docview/2215248827?pq-origsite=primo&accountid=9630.

Valdarrama, Santiago. 2024. “Sorting Algorithms in Python.” Real Python. https://realpython.com/sorting-algorithms-python/.

Vincent, James. 2020. “Scientists Rename Human Genes to Stop Microsoft Excel from Misreading Them as Dates.” The Verge, August. https://www.theverge.com/2020/8/6/21355674/human-genes-rename-microsoft-excel-misreading-dates.

Ziemann, Mark, Yotam Eren, and Assam El-Osta. 2016. “Gene Name Errors Are Widespread in the Scientific Literature.” Genome Biology 17 (1): 1–3.

🗓️ Week 03 Computational Thinking and Programming

Excel…

Mentimeter: What do you think of Excel?

Mentimeter: Excel mishaps

The Excel Problem

Horror Story #1: Gene Names

Horror Story #2: COVID-19 Data Loss

Horror Story #3: Economic Policy

Horror Story #4: The London Whale

Horror Story #4: The London Whale

Horror Story #5: Microsoft and Finance

The Excel Takeaway

Excel wrap-up Mentimeter 💭

What do these stories have in common?

It’s not about Excel…

From Chaos to Clarity

Computational Thinking

Mentimeter quiz

What is computational thinking? 🧠

Two Aspects of Computational Thinking

Schelling Model – How it works

Schelling Model – Computational Thinking Takeaway

Try It Yourself: Making Tea ☕

Tea Algorithm ☕

What is an algorithm? 📊

Sorting…

🎯 Action Point

Time for a break 🍵

Time to look at another example of algorithm

Dijkstra’s Algorithm – Step by Step Solution

Dijkstra’s Algorithm – Step by Step Solution

Dijkstra’s Algorithm – Step by Step Solution

Dijkstra’s Algorithm – Step by Step Solution

Dijkstra’s Algorithm – Step by Step Solution

Dijkstra’s Algorithm – Step by Step Solution

Dijkstra’s Algorithm – Step by Step Solution

Dijkstra’s algorithm in words

Use cases for shortest path algorithms (and Dijkstra algorithm)

Time for some voting! 🗳️

Voting: a breakdown

Voting algorithms in words

Time for assigning tasks!

How does the Hungarian algorithm work?

How does the Hungarian algorithm work?

How does the Hungarian algorithm work?

How does the Hungarian algorithm work?

How does the Hungarian algorithm work?

Hungarian algorithm Summary

Some resources to go further

References

🗓️ Week 03
Computational Thinking and Programming