flowchart LR
A(Input) --> B{Set of instructions/rules</br>to obtain the expected</br> output from the given input}
B --> C(Output)
🗓️ Week 03
Computational Thinking and Programming
DS101 – Fundamentals of Data Science
14 Oct 2024
Course rep volunteers needed!

DSI Quiz Social

Tuesday 15th October 5pm DSI Visualisation Studio, Col.1.06
Form to sign in here
Computational Thinking
What is computational thinking?
The mental skills and practices related to the following aspects of computing:
1️⃣ Designing computations that get computers to do the jobs for us
2️⃣ Explaining and interpreting the world as a complex information process
1️⃣ Designing computations
We usually have to think like computers to design the proper computations for the job.
- Input: numbers, symbols, lists
- Output: a solution
- Computation: deterministic calculations & symbolic manipulation
2️⃣ Explaining and interpreting the world
We can use computers to create models of the world.
Let us look at a simple, old example of a computational model for urban segregation (McCown 2014) ➡️
What is computational thinking?
Today our focus is on the first aspect:
1️⃣ Designing computations that get computers to do the jobs for us
2️⃣ Explaining and interpreting the world as a complex information process
Algorithms
Recipes for computers

Algorithms
- Clear and unambiguous: Each step of the algorithm should have one unambiguous meaning
- Finiteness: The algorithm is finite i.e it terminates after a finite time
- Language independent: the algorithm is composed of a set of instructions that can be implemented in any programming language and still lead to the same outcome
- Feasible: The algorithm must be simple, generic and practical so to be executed with the resources available. It cannot depend on future or non-existing technologies.
graph LR B((Algorithm characteristics))-->A(Well-defined inputs) B--> C(Well-defined outputs) B-->D(Clear and unambiguous) B-->E(Finiteness) B-->F(Language-independent) B-->G(Feasible)
Let’s look at an every day example
Home temperature control
How would a simple home heating system work?
algorithm home_temperature_control is:
input:
Heating system state s;
Temperature reading frequency f;
Upper temperature threshold Tupper;
Lower temperature threshrold Tlower;
while (s=='active') do
current_temperature=read(temperature every f seconds)
if current_temperature < Tlower:
turn heating on
else if current_temperature > Tupper:
turn heating off
else if current_temperature >= Tlower and current_temperature <= Tupper:
maintain current heating state
Let’s look at a classic computer science example
Problem Definition:
Whenever I receive a list of numbers, I want to ensure this list is ordered.

Breakdown
Input:
[10, 20, 42, 29, 50]
Output:
[10, 20, 29, 42, 50]
Computation:
How would you solve it❓
🎯 Action Point
Group up with the people of your respective tables and try to come up with a recipe that solves the problem, regardless of the list size.
Test that your recipe works for the following list:
[237, 153, 311, 33, 854, 212, 368, 42, 892, 755]Time for a break 🍵

After the break:
- Other algorithm examples
Time to look at another example of algorithm
graph LR A(A) ---|2| B(B) B ---|5| D(D) A ---|6| C(C) C ---|8| D D ---|10| E(E) D ---|15| F(F) F ---|6| E E ---|2| G(G) F ---|6| G
Graph:
- Nodes (A, B,C,…)
- Edges (Undirected, weighted)
🎯 How do we get the shortest path between A and all the other nodes in this graph (i.e between A and B, A and D, A and G, etc…?
Pair with the people in your respective tables and discuss.
One possible solution: The Dijkstra algorithm
Step 1: Mark the source node with a current distance of 0 and the rest with infinity
Step 2: Set the non-visited node with the smallest current distance, as the current node, let’s say c (initially c is set to the source node).
Step 3: For each neighbour N of the current node c: add the current distance of c with the weight of the edge c-N. If it is smaller than the current distance of N, set it as the new current distance of N.
Step 4: Mark c as visited.
Step 5: Go to Step 2 if there are any unvisited nodes.
A visual summary of the Dijkstra algorithm
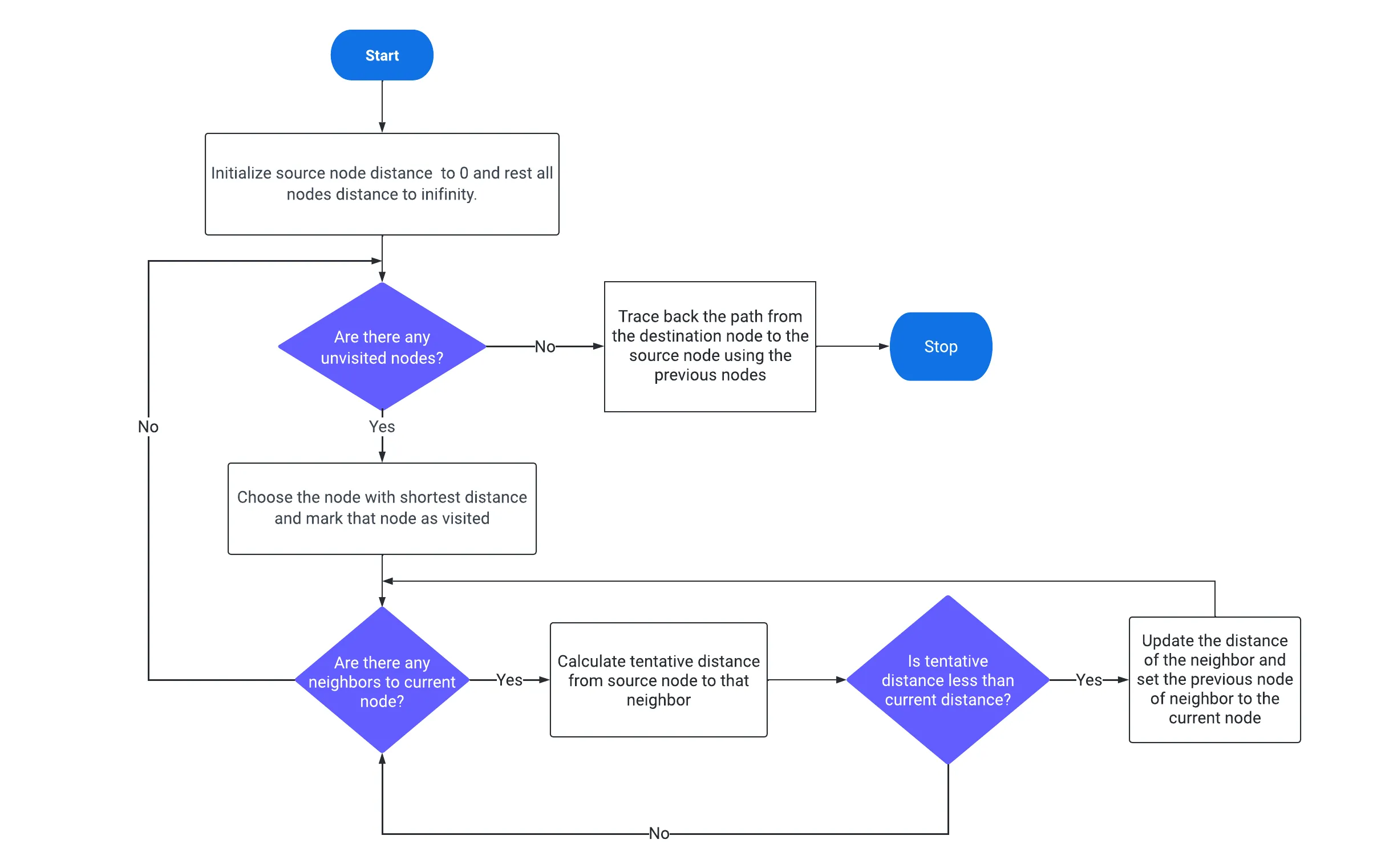
Applying Dijkstra on our example graph
graph LR A(A) ---|2| B(B) B ---|5| D(D) A ---|6| C(C) C ---|8| D D ---|10| E(E) D ---|15| F(F) F ---|6| E E ---|2| G(G) F ---|6| G
Source node: A
- Initially :
| A | B | C | D | E | F | G | |
|---|---|---|---|---|---|---|---|
| Distance | 0 | \(\infty\) | \(\infty\) | \(\infty\) | \(\infty\) | \(\infty\) | \(\infty\) |
Unvisited nodes: {A,B,C,D,E,F,G}
- Updating distance of nodes adjacent to A i.e B and C
| A | B | C | D | E | F | G | |
|---|---|---|---|---|---|---|---|
| Distance | 0 | 2 | 6 | \(\infty\) | \(\infty\) | \(\infty\) | \(\infty\) |
Closest node to source node (based on current distances): B
nodes on path: {A, B}
Unvisited nodes: {A,B,C,D,E,F,G}
- Next : C and D (adjacent to A and B)
| A | B | C | D | E | F | G | |
|---|---|---|---|---|---|---|---|
| Distance | 0 | 2 | 6 | 7 | \(\infty\) | \(\infty\) | \(\infty\) |
Unvisited nodes: {A,B,C,D,E,F,G}
Applying Dijkstra on our example graph
graph LR A(A) ---|2| B(B) B ---|5| D(D) A ---|6| C(C) C ---|8| D D ---|10| E(E) D ---|15| F(F) F ---|6| E E ---|2| G(G) F ---|6| G
- Next node : D (adjacent to B and C)
| A | B | C | D | E | F | G | |
|---|---|---|---|---|---|---|---|
| Distance | 0 | 2 | 6 | 7 (via B not C 14) | \(\infty\) | \(\infty\) | \(\infty\) |
Unvisited nodes: {A,B,C,D,E,F,G}
- Next : nodes E and F
| A | B | C | D | E | F | G | |
|---|---|---|---|---|---|---|---|
| Distance | 0 | 2 | 6 | 7 (via B not C 14) | 17 (A–B–D–E) | 22 (A–B–D–F) | \(\infty\) |
Unvisited nodes: {A,B,C,D,E,F,G}
Applying Dijkstra to our graph example
graph LR A(A) ---|2| B(B) B ---|5| D(D) A ---|6| C(C) C ---|8| D D ---|10| E(E) D ---|15| F(F) F ---|6| E E ---|2| G(G) F ---|6| G
- Next : nodes F and G
| A | B | C | D | E | F | G | |
|---|---|---|---|---|---|---|---|
| Distance | 0 | 2 | 6 | 7 (via B not C 14) | 17 (A–B–D–F) | 22 (A–B–D–E) | 19 (A–B–D–F–G) |
For F: distance unchanged since second option (A–B–D–F–E) more costly (23 instead of 22)
Unvisited nodes: {A,B,C,D,E,F,G}
- Last unvisited node: F
| A | B | C | D | E | F | G | |
|---|---|---|---|---|---|---|---|
| Distance | 0 | 2 | 6 | 7 (via B not C 14) | 17 (A–B–D–E) | 22 (A–B–D–F) | 19 (A–B–D–F–G) |
Possibilities: 22 (A–B–D–F), 23 (A–B–D–E–F), 25 (A–B–D–E–G–F)
Previous distance from (A–B–D–F) unchanged since lowest
No more unvisited nodes
Final shortest distance calculation from A to other nodes
| A | B | C | D | E | F | G | |
|---|---|---|---|---|---|---|---|
| Distance | 0 | 2 | 6 | 7 | 17 | 22 | 19 |
Use cases for the Dijkstra algorithm
What could be potential meanings of our example graph?
graph LR Home(Home) ---|2| B(Bus Stop) B(Bus Stop) ---|5| Park(Park) Home ---|6| T(Train Station) Park ---|8| T T ---|10| Supermarket(Supermarket) T ---|15| GP(GP) GP ---|6| Supermarket Supermarket ---|2| University(University) GP ---|6| University
Use cases for the Dijkstra algorithm
What could be potential meanings of our example graph?
graph LR London(London) ---|"2£"| Cambridge(Cambridge) Cambridge ---|"5£"| Luton(Luton) London ---|"6£"| Gatwick(Gatwick) Luton ---|"8£"| Gatwick Gatwick ---|"15£"| Amsterdam(Amsterdam) Gatwick ---|"10£"| Paris(Paris) Paris ---|"6£"| Amsterdam Amsterdam ---|"2£"| Berlin(Berlin) Paris ---|"6£"| Berlin
Use cases for Dijkstra: Movie recommendation
Say we have this table that represents ratings that some users gave to some movies currently airing in the UK:

💭 How does this table translate to a graph?
Use cases for Dijkstra: Movie recommendation
The paths per user are:
U1: Beetlejuice Beetlejuice:4.5 \(->\) Speak No Evil:2 \(->\) The Critic:3.5
U2: Beetlejuice Beetlejuice:2.5 \(->\) Transformers One:3 \(->\) Speak No Evil: 4 \(->\) The Critic:4
U3: Beetlejuice Beetlejuice:3 \(->\) The Critic:3.5
U4: Transformers One:5 \(->\) The Critic:4
U5: Beetlejuice Beetlejuice:4 \(->\) Transformers One:2 \(->\) Speak No Evil:3 \(->\) The Critic:2
Assuming the movies are the graph nodes, we have to somehow find a way to convert the user ratings into edge weights (or “costs”).
Use cases for Dijkstra: Movie recommendation
Supposing we denote as:
- \(v\) and \(v'\) two connected vertices/nodes
- \(r_{iv}\) and \(r_{iv'}\) the ratings given by the \(i\)th user
- \(w_{r_i}\) the weight of a user’s opinion (could be reduced in case user who is too profilific a rater)
- \(w_v'\) the global weight of a recommendation candidate (could be reduced if a movie is too popular)
one way of calculating the cost would be the following:
\[ \begin{equation} L_{vv'}=\frac{1}{\sum_{i=1}^n\frac{w_{r_i}w_v'}{\exp{|r_{iv}-r{iv'}|}}} \end{equation} \]
Use case for Dijkstra: movie recommendation
Here is the graph we end up with!
graph LR B(Beetlejuice Beetlejuice) ---|1.348| T(Transformers One) B ---|1.649| C(The Critic) B ---|12.18| S(Speak No Evil) S ---|1.359| T S---|0.628| C C ---|2.718| T
Use cases for shortest path algorithms (and Dijkstra algorithm)
- find optimal directions between locations (e.g Google Maps-see here for a further explanation)/GPS Navigation: considering real-traffic conditions, calculate the shortest path between a source and destination in navigation systems
- determine the shortest path between network nodes, helping in efficiently routing data packets (used in computer networks but also telephone networks)
- recommendation systems: find the most relevant and shortest path between items or users
- social networks: suggest a list of friends that a user may know
Another algorithm: Assignment problem
Suppose you are working as an engineer at Uber and you need to find a way to match drivers with clients. How do you go about doing that?
A solution: the Hungarian algorithm!
How does the Hungarian algorithm work?
Suppose you have a table that represents the “cost” of each job (i.e picking up a client) per driver:
| Job 1 | Job 2 | Job 3 | |
|---|---|---|---|
| Driver A | 10 | 15 | 9 |
| Driver B | 9 | 18 | 5 |
| Driver C | 6 | 14 | 3 |
Step 1 — Subtract the minimum from every element of each row
| Job 1 | Job 2 | Job 3 | |
|---|---|---|---|
| Driver A | 10 | 15 | 9 |
| Driver B | 9 | 18 | 5 |
| Driver C | 6 | 14 | 3 |
\(->\)
| Job 1 | Job 2 | Job 3 | |
|---|---|---|---|
| Driver A | 1 | 6 | 0 |
| Driver B | 4 | 13 | 0 |
| Driver C | 3 | 11 | 0 |
How does the Hungarian algorithm work?
Step 2 — Subtract the minimum of each column
| Job 1 | Job 2 | Job 3 | |
|---|---|---|---|
| Driver A | 1 | 6 | 0 |
| Driver B | 4 | 13 | 0 |
| Driver C | 3 | 11 | 0 |
\(->\)
| Job 1 | Job 2 | Job 3 | |
|---|---|---|---|
| Driver A | 0 | 0 | 0 |
| Driver B | 3 | 7 | 0 |
| Driver C | 2 | 5 | 0 |
Step 3 — Cross 0s with the minimum number of lines needed.
❌
| Job 1 | Job 2 | Job 3 | |
|---|---|---|---|
| Driver A | |||
| Driver B | |||
| Driver C |
✅
| Job 1 | Job 2 | Job 3 | |
|---|---|---|---|
| Driver A | |||
| Driver B | 3 | 7 | |
| Driver C | 2 | 5 |
If the number of lines is < \(n\), the number of rows and columns in the matrix, reduce the matrix again (i.e step 4). In our example, we have 2 lines, but we have a 3x3 matrix, so we’ll reduce again. If we didn’t have this case, we’d directly jump to step 5.
How does the Hungarian algorithm work?
Step 4 — Find the smallest entry not covered by any line, and subtract this entry from the entire non-crossed matrix (and add it to the elements crossed twice).
| Job 1 | Job 2 | Job 3 | |
|---|---|---|---|
| Driver A | |||
| Driver B | 3 | 7 | |
| Driver C | 2 | 5 |
\(->\)
| Job 1 | Job 2 | Job 3 | |
|---|---|---|---|
| Driver A | |||
| Driver B | 1 | 5 | |
| Driver C | 0 | 3 |
then go back to step 3: cross the 0s!
| Job 1 | Job 2 | Job 3 | |
|---|---|---|---|
| Driver A | |||
| Driver B | 1 | 5 | |
| Driver C |
This time, we have three lines so we can go to step 5.
How does the Hungarian algorithm work?
Step 5 — Assign Jobs and Workers starting with the line with only one zero!
| Job 1 | Job 2 | Job 3 | |
|---|---|---|---|
| Driver A | 0 | 0 | 2 |
| Driver B | 1 | 5 | 0 |
| Driver C | 0 | 3 | 0 |
- We start with the line with only one zero (there’s only one!) and assign its job to the corresponding driver i.e Job 3 to Driver B. We then cross its row and column to make it unavailable.
- The row that then contains a single zero corresponds to Driver C for Job 1: so Job 1 is assigned to Driver C. Again, we cross the corresponding row and column.
- We’re left with Job 2 for Driver A. And so, we have our optimal assignment!
Some resources to go further
References

LSE DS101 2024/25 Autumn Term