🗓️ Week 07
Machine Learning I

DS101 – Fundamentals of Data Science

Dr. Ghita Berrada

LSE Data Science Institute

06 Nov 2023

What we will cover today:

• ⏪ Recap
• What is Machine Learning?
• Supervised Learning
• Algorithms
• What’s next?

⏪ Recap

• A model is a mathematical representation of a real-world process, a simplified version of reality.
• We saw examples of a linear regression model.
  • It contains several assumptions that need to be met for the model to be valid.
  • Social scientists have been using linear regression models for decades.

• It is a widely used statistical technique for exploring the relationship between a (numeric) response variable and one or more explanatory variables.

⏪ Recap: Linear Regression

We also saw how linear regression models are normally represented mathematically:

The generic supervised model:

\[ Y = \operatorname{f}(X) + \epsilon \]

is defined more explicitly as follows ➡️

Simple linear regression

\[ \begin{align} Y = \beta_0 +& \beta_1 X + \epsilon, \\ \\ \\ \end{align} \]

when we use a single predictor, \(X\).

Multiple linear regression

\[ \begin{align} Y = \beta_0 &+ \beta_1 X_1 + \beta_2 X_2 \\ &+ \dots \\ &+ \beta_p X_p + \epsilon \end{align} \]

when there are multiple predictors, \(X_p\).

Note

• As a well-studied statistical technique, we know a lot about the properties of the model.
• Researchers can use this knowledge to assess the validity of the model, using things like confidence intervals, hypothesis testing, and many other model diagnostics.

• End the slide with: what about the limitations of linear regression models?

Limitations of Linear Regression Models

The typical linear model assumes that:

• the relationship between the response and the predictors is linear.
• the error terms are independent and identically distributed.
• the error terms have a constant variance.
• the error terms are normally distributed.

Important

Barely any real-world process is linear.

Making Predictions

We often want to use a model to make predictions

• either about the future
• or about new observations.

⏪ The simple linear model from W05

Remember the simple linear model from W05?

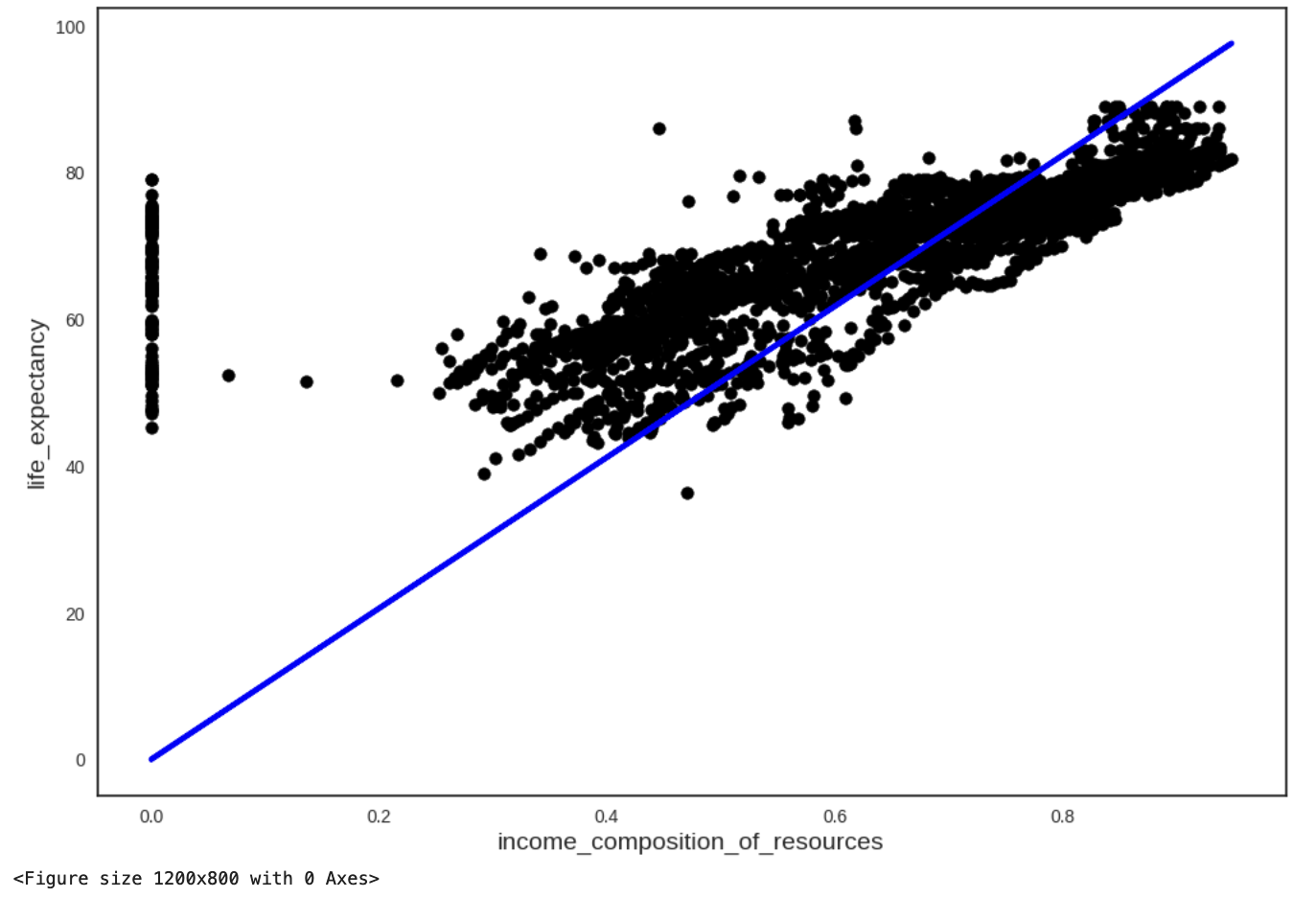
What happens when we extrapolate?

What kind of prediction would this model give if we were to set the independent variable to 1 (i.e maximum possible human development index) ?

What happens when we extrapolate?

What kind of prediction would this model give if we were to set the independent variable to 1 (i.e maximum possible human development index) ?

Since the model equation was: \[\begin{align} \operatorname{life\_expectancy} = & 102.9273 \times \operatorname{income\_composition\_of\_resources} \end{align}\]

this means a human development index of 1 (i.e income_composition_of_resources=1) means a life expectancy of 102.9273 years!

The thing about predictions

• We can use a model to make predictions about the future.
• We can also use a model to make predictions about new observations.
• But we need to be careful about the assumptions that we make about the data.

Note

We will focus a lot more on predictions from now on.

This is because Machine Learning, in practice, is all about making predictions.

• I highlight assumptions because this is often overlooked by ML practitioners.
• Thinking about assumptions, or the lack of them, is a main topic of this course.

What is Machine Learning?

A definition

Machine Learning (ML) is a subfield of Computer Science and Artificial Intelligence (AI) that focuses on the design and development of algorithms that can learn from data.

How it works

https://xkcd.com/1838

How it works

• The process is similar to the regular algorithms (think recipes) we saw in W03.
• Only this time, the ingredients are data.

INPUT (data)

⬇️

ALGORITHM

⬇️

OUTPUT (prediction)

Types of Machine Learning

Supervised
Learning

• Each data point is associated with a label.
• The goal is to learn a function that maps the data to the labels.

(🗓️ Week 07)

Unsupervised
Learning

• There is no such association between the data and the labels.
• The focus is on similarities between data points.

(🗓️ Week 08)

Supervised Learning

Supervised Learning

If we assume there is a way to map between X and Y, we could use SUPERVISED LEARNING to learn this mapping.

Supervised Learning

• The algorithm will teach itself to identify changes in \(Y\) based on the values of \(X\)​
• A dataset of labelled data is required​
• Prediction: presented with new \(X\), the algorithm will be able to predict how \(Y\) would be like​

Supervised Learning

• If \(Y\) is a numerical value, we call it a regression problem.​
• If \(Y\) is a category, we call it a classification problem.​

Supervised Learning

• There are countless ways to do that; each algorithm does it in its own way.​
• Here are some names of basic algorithms:​
  • Linear regression​
  • Logistic regression​
  • Decision trees​
  • Support vector machines​
  • Neural networks​

One Practical Example

Suppose you want to be able to tell whether a patient has breast cancer or not.

How would you approach this problem?

What is in the digitized images of biopsies?

Source: (Zheng et al. 2013)

About 30 features, among which for each cell nucleus (3), 10 features:

• radius (mean of distances from center to points on the perimeter)
• texture (standard deviation of gray-scale values)
• perimeter
• area
• smoothness (local variation in radius lengths)
• compactness (perimeter^2 / area - 1.0)
• concavity (severity of concave portions of the contour)
• concave points (number of concave portions of the contour)
• symmetry
• fractal dimension (“coastline approximation” - 1)

All of this information constitutes our input.

• Note that you might need to transform the data first.
• For example, you might want to extract the date from the description.

What about the output?

• The output is something you would normally want to predict or attempt to explain​ ¹
• Also referred to as the label, “ground truth”, target or dependent variable, or simply \(Y​\)
• Most commonly it is a numerical or categorical variable​

1. See “To Explain or To Predict?” (Shmueli 2010)​

Structure of dataset

Side story

• The data shown before actually corresponds to the Diagnostic Wisconsin Breast Cancer Database¹ (Wolberg and Street 1995) that was made publicly available (in 1995!) on the UC Irvine Machine Learning Repository (or UCI Machine Learning Repository).

• The UCI repository is “a collection of databases, domain theories, and data generators that are used by the machine learning community for the empirical analysis of machine learning algorithms” ((Markelle Kelly, n.d.), “About Us” page).

https://archive.ics.uci.edu

1. You’ll get to practice supervised learning techniques with this dataset during this week’s class! 🤺

Time for a break 🍵

After the break:

• Examples of supervised learning algorithms
• Self-supervised learning

Algorithms

The Logistic Regression model

Consider a binary response:

\[ Y = \begin{cases} 0 \\ 1 \end{cases} \]

We model the probability that \(Y = 1\) using the logistic function (aka. sigmoid curve):

\[ Pr(Y = 1|X) = p(X) = \frac{e^{\beta_0 + \beta_1X}}{1 + e^{\beta_0 + \beta_1 X}} \]

• This is how this function looks like

The Decision Tree model

The Support Vector Machine model

The Support Vector Machine model

Say you have a dataset with two classes of points:

The Support Vector Machine model

The goal is to find a line that separates the two classes of points:

The Support Vector Machine model

It can get more complicated than just a line:

• Explain the dataset

Neural Networks

Deep Learning

• Stack a lot of layers on top of each other, and you get a deep neural network.
• Forget about interpretability!

Attention

• The Transformer architecture is a deep learning model that uses attention to learn contextual relationships between words in a text.
• It has revolutionized the field of Natural Language Processing (NLP).

What’s next?

What’s next?

• 🗓️ Week 08: Unsupervised learning
• 🗓️ Week 09: More on unstructured data
  • You will also explore how to measure the performance of your models
• 🗓️ Week 10: We’ll think deeper about what it means to predict something
  • We’ll also talk about fairness and bias in machine learning

References

Markelle Kelly, Kolby Nottingham, Rachel Longjohn. n.d. “The UCI Machine Learning Repository.” https://archive.ics.uci.edu.

Shmueli, Galit. 2010. “To Explain or to Predict?” Statistical Science 25 (3). https://doi.org/10.1214/10-STS330.

Wolberg, Mangasarian, William, and W. Street. 1995. “Breast Cancer Wisconsin (Diagnostic).” UCI Machine Learning Repository.

Zheng, Jiamin, Tahra Alsaadi, Jason Blaichman, Xuanqian Xie, Attila Omeroglu, Sarkis Meterissian, and Benoı̂t Mesurolle. 2013. “Invasive Ductal Carcinoma of the Breast: Correlation Between Tumor Grade Determined by Ultrasound-Guided Core Biopsy and Surgical Pathology.” American Journal of Roentgenology 200 (1): W71–74.