🗓️ Week 05
Statistical Inference II

DS101 – Fundamentals of Data Science

Dr. Jon Cardoso-Silva

LSE Data Science Institute

13 Feb 2023

What we will cover today:

• Dependent variable
• Independent variables
• Modelling
• Now for something (slightly) different

Statistical Inference I & II

What we will talk about this week:

🗓️ Week 04

• Samples, Population & Resampling
• Exploratory Data Analysis
• Correlation vs Causation
• What is Probability?
• Probability Distributions

🗓️ Week 05

• Hypothesis Testing
• Framing Research Questions
• Randomised Controlled Trials
• A/B Tests
• What about Cause and Effect?

Our Case Study

The LivWell dataset

Belmin, Camille, Roman Hoffmann, Mahmoud Elkasabi, and Peter-Paul Pichler. 2022. “LivWell: A Sub-National Database on the Living Conditions of Women and Their Well-Being for 52 Countries. Zenodo. https://doi.org/10.5281/ZENODO.7277104.

– (Belmin et al. 2022a) & (Belmin et al. 2022b)

What is the goal?

• Let’s use the LivWell dataset to illustrate the concepts of traditional statistical inference
  • for example confidence intervals and hypothesis testing
• We want to create a model to explain the relationship between what we call:
  • the independent variables and
  • the dependent variable

Indicator Categories

library(tidyverse)
library(livwelldata)

livwell_indicators() %>% 
  group_by(indicator_category) %>% 
  tally() %>% 
  arrange(desc(n))

indicator_category	n
Precipitation	42
Standardized Precipitation Evapotranspiration Index (SPEI)	39
Temperature	39
Individual demographic information	18
Energy and information	12
Household characteristics - Household level	11
Reproductive health and fertility	11
Decision power	10
Domestic Violence	10
Drought	9
Education	9
Fertility - complex indicators	9
Household characteristics - Womens level	9
Energy and information - Household level	7
Health	7
Health - Birth level	5
Work status	4
Fertility preferences	3
Household Wealth	3
Energy and information - per urban/rural area	2
Household demographics - Household level	2
Socio-economic indicators	2
Household household demographics - Household level	1
Nutrition	1

Variables related to Decision power

livwell_indicators() %>% 
  filter(indicator_category == "Decision power") %>% 
  select(indicator_name, indicator_description)

indicator_code	indicator_description
DP_decide_money_p	Women currently married or in union who were paid cash for their work, who decide alone how their money earned is spent (%)
DP_decide_health_p	Women who have the final say on their health care (%)
DP_decide_large_purchase_p	Women who have the final say on large household purchases(%)
DP_decide_visits_p	Women who have the final say on visiting family or relatives (%)
DP_decide_contraception_p	Women deciding alone on their contraception (%)
DP_decide_no_contraception_p	Women deciding alone on not using contraception (%)
DP_owns_house_p	Women owning a house alone or jointly (%)
DP_owns_land_p	Women owning land alone or jointly (%)
DP_earn_more_equal_p	Women currently married or in union who were paid cash for their work, earning more or equal than her partner (%)
DP_earn_more_p	Women currently married or in union who were paid cash for their work, earning more than her partner (%)

Dependent variable

The dependent variable

Inspecting missing values:

Some more pre-processing…

I created a sort of algorithm to identify the best interval to use for modelling the DP_decide_health_p variable.

Step 1

• First, calculate years for which we have data for each country:

df <- 
    # Get data for the DP_decide_health_p variable
    livwell_data(indicator_codes=c("DP_decide_health_p"), interpolate="linear") %>% 
    # Remove rows with missing values
    filter(!is.na(DP_decide_health_p)) %>% 
    group_by(country_code) %>% 
    # Calculate years for which we have data
    summarise(minYear=min(year), maxYear=max(year)) %>% 
    arrange(minYear, desc(maxYear))
df %>% head()

country_code	minYear	maxYear
ZWE	1999	2015
ARM	2000	2016
HTI	2000	2016
UGA	2000	2016
COL	2000	2015
MWI	2000	2015

Step 2

• Then, compute all possible intervals of years for which we have data for each country:

abs_min_year <- df %>% pull(minYear) %>% min()
abs_max_year <- df %>% pull(maxYear) %>% max()

df_intervals <- expand.grid(interval=seq(abs_min_year, abs_max_year, by=1), 
                            interval_length=seq(1, abs_max_year-abs_min_year+1, by=1)) %>% 
    filter(interval+interval_length-1 <= abs_max_year) %>% 
    mutate(interval_end=interval+interval_length-1) %>%
    filter(interval_length > 1)

interval	interval_length	interval_end
1999	2	2000
2000	2	2001

…

interval	interval_length	interval_end
2000	20	2019
1999	21	2019

Step 3

• Finally, for each interval of years, compute the number of countries for which we have data.
• Select years for which we have data for most countries:

# For each row in df_intervals, compute the number of countries that have data for that interval
df_intervals %>% 
    rowwise() %>% 
    mutate(n_countries=sum(df$minYear>=interval & df$maxYear<=interval_end)) %>%
    arrange(desc(n_countries)) %>%
    head(10)

Step 3 (output)

interval	interval_length	interval_end	n_countries
1999	21	2019	50
2000	20	2019	49
1999	20	2018	48
2000	19	2018	47
1999	19	2017	43
2000	18	2017	42
2001	19	2019	42
2001	18	2018	40
2002	18	2019	38
2003	17	2019	37

What does this mean?

• I have chosen to use the interval of years 1999-2019 for modelling the DP_decide_health_p variable.
• This interval of years is the one for which we have data for most countries and regions.

🗣️ Point of discussion

Is it possible that I am introducing some bias by choosing this interval of years?

Distribution

Described by the median and interquartile range:

Distribution

Described the mean and standard deviation:

Independent variables

What could help us predict the DP_decide_health_p variable?

Independent variables

I semi-randomly selected 42 independent variables that could help us predict the DP_decide_health_p variable:

livwell_indicators(category_contains = c("household", "education")) %>% 
    select(indicator_description)

Independent variables (output)

indicator_description
Average time to get to drinking water
Women living in households with high quality toilet facility (%)
Women living in households with low quality toilet facility (%)
Women living in a household with high quality floor (%)
Women living in a household with low quality floor (%)
Women living in a household with high quality water access (%)
Women living in a household with low quality water access (%)
Average number of household members
Average number of children resident in the household under the age of 5
Female average/median years of schooling
Women with no education (%)
Women with primary education (%)
Women with completed primary education (%)
Women with secondary education (%)
Women with completed secondary education (%)
Women with secondary education or higher education(%)
Women who can read a whole sentence (%)
Women who are literate (%)
Average time to get to drinking water
Households with high quality toilet facility (%)
Households with low quality toilet facility (%)

indicator_description
Households with high quality floor (%)
Households with low quality floor (%)
Households with high quality water access (%)
Households with low quality water access (%)
Households with watch (%)
Households with car (%)
Households with motorcycle (%)
Households with bicycle (%)
Average number of household members
Average number of household members
Average number of children resident in the household under the age of 5
Households with electricity (%)
Households with tv (%)
Households with radio (%)
Households with fridge (%)
Households with a telephone (%)
Households whose main cooking fuel is modern (%)
Households with computer (%)
Average of the International Wealth Index
Median of the International Wealth Index
GINI coefficient of the International Wealth Index

More pre-processing

• Some of these variables had too many missing values, so I removed them.
• The resulting 19 variables are:

indicator_code	indicator_category	indicator_description
ED_educ_years_mean	Education	Female average/median years of schooling
ED_attainment_no_educ_p	Education	Women with no education (%)
ED_attainment_primary_p	Education	Women with primary education (%)
ED_attainment_primary_completed_p	Education	Women with completed primary education (%)
ED_attainment_secondary_p	Education	Women with secondary education (%)
ED_attainment_secondary_higher_p	Education	Women with secondary education or higher education(%)
ED_litt_p	Education	Women who are literate (%)
EI_tv_p	Energy and information - Household level	Households with tv (%)
EI_radio_p	Energy and information - Household level	Households with radio (%)
WL_wealth_mean	Household Wealth	Average of the International Wealth Index
WL_wealth_median	Household Wealth	Median of the International Wealth Index
WL_wealth_gini	Household Wealth	GINI coefficient of the International Wealth Index
HH_floor_high_p	Household characteristics - Household level	Households with high quality floor (%)
HH_floor_low_p	Household characteristics - Household level	Households with low quality floor (%)
HD_women_size_mean	Household characteristics - Women’s level	Average number of household members
HD_women_children_mean	Household characteristics - Women’s level	Average number of children resident in the household under the age of 5
HD_size_defacto_mean	Household demographics - Household level	Average number of household members
HD_children_mean	Household demographics - Household level	Average number of children resident in the household under the age of 5
HD_size_dejure_mean	Household household demographics - Household level	Average number of household members

Correlation matrix

More pre-processing

• I removed the variables that were highly correlated with each other.
• The resulting 7 variables are:

New correlation matrix

Modelling

• A model is a mathematical representation of a real-world process, a simplified version of reality.
• Let’s look at one simple modelling algorithm: linear regression.

What is Linear Regression

The generic supervised model:

\[ Y = \operatorname{f}(X) + \epsilon \]

is defined more explicitly as follows ➡️

Simple linear regression

\[ \begin{align} Y = \beta_0 +& \beta_1 X + \epsilon, \\ \\ \\ \end{align} \]

when we use a single predictor, \(X\).

Multiple linear regression

\[ \begin{align} Y = \beta_0 &+ \beta_1 X_1 + \beta_2 X_2 \\ &+ \dots \\ &+ \beta_p X_p + \epsilon \end{align} \]

when there are multiple predictors, \(X_p\).

Warning

• True regression functions are never linear!
• Although it may seem overly simplistic, linear regression is extremely useful both conceptually and practically.

Linear Regression with a single predictor

We assume a model:

\[ Y = \beta_0 + \beta_1 X + \epsilon , \]

where:

• \(\beta_0\): an unknown constant that represents the intercept of the line.
• \(\beta_1\): an unknown constant that represents the slope of the line
• \(\epsilon\): the random error term (irreducible)

\(\beta_0\) and \(\beta_1\) are also known as coefficients or parameters of the model.

Linear Regression with a single predictor

We want to estimate:

\[ \hat{y} = \hat{\beta_0} + \hat{\beta_1} x \]

where:

• \(\hat{y}\): is a prediction of \(Y\) on the basis of \(X = x\).
• \(\hat{\beta_0}\): is an estimate of the “true” \(\beta_0\).
• \(\hat{\beta_1}\): is an estimate of the “true” \(\beta_1\).

The hat symbol denotes an estimated value.

Back to our case study

# Fit a linear model
model <- lm(DP_decide_health_p ~ ED_educ_years_mean, data = df)

summary(model)

Call:
lm(formula = DP_decide_health_p ~ ED_educ_years_mean, data = df)

Residuals:
    Min      1Q  Median      3Q     Max 
-49.522  -9.336  -1.670   7.664  59.391 

Coefficients:
                   Estimate Std. Error t value Pr(>|t|)    
(Intercept)         8.48552    0.51705   16.41   <2e-16 ***
ED_educ_years_mean  3.40716    0.07565   45.04   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 14.72 on 4485 degrees of freedom
Multiple R-squared:  0.3114,    Adjusted R-squared:  0.3113 
F-statistic:  2028 on 1 and 4485 DF,  p-value: < 2.2e-16

\[\begin{align} \operatorname{DP\_decide\_health\_p} =& \\ &+3.41 \times \operatorname{ED\_educ\_years\_mean}\\ &+8.49 \end{align}\]

🤔 What does all of this mean?

Visualising the model

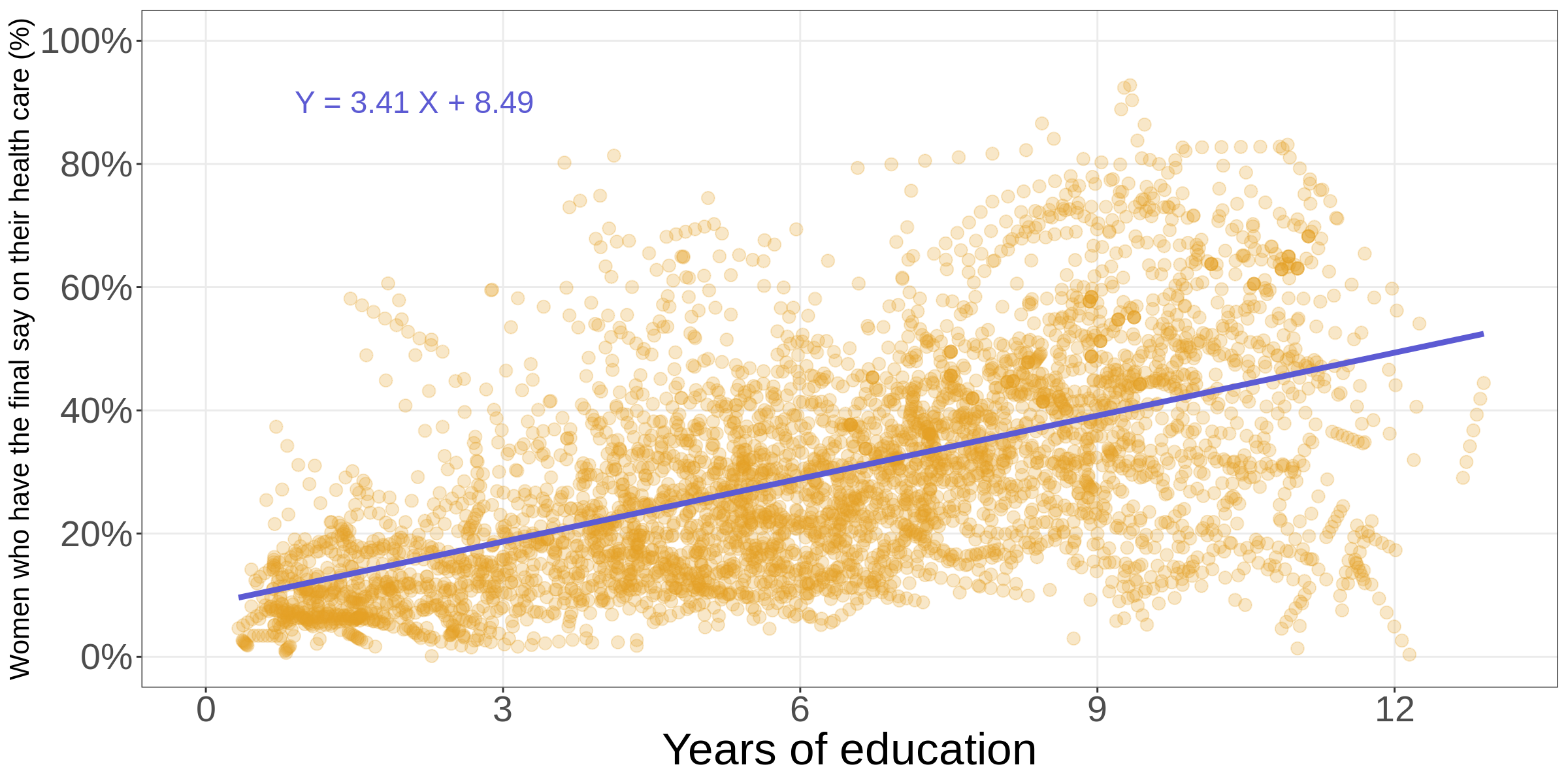
What about confidence intervals?

• If we were to fit a linear model from repeated samples of the data, we would get different coefficients every time.
• Because of the Central Limit Theorem, we know that the mean of this sampling distribution can be approximated by a Normal Distribution.
• We know from Normal Theory that 95% of the distribution lies within two times the standard deviation (centred around the mean).
  

A 95% confidence interval is defined as a range of values such that with 95% probability, the range will contain the true unknown value of the parameter.

Back to our example

One can calculate the confidence intervals for the coefficients using the confint() function in R:

confint(model, level=0.95)

	2.5 %	97.5 %
(Intercept)	7.471849	9.499181
ED_educ_years_mean	3.258841	3.555471

Hypothesis testing

• The idea of confidence intervals is closely related to the idea of hypothesis testing.
• The most common hypothesis test involves testing the null hypothesis of:
  • \(H_0\): There is no relationship between \(X\) and \(Y\) versus the .
  • \(H_A\): There is some relationship between \(X\) and \(Y\).

• Mathematically, this corresponds to testing:

\[ \begin{align} &~~~~H_0:&\beta_1 &= 0 \\ &\text{vs} \\ &~~~~H_A:& \beta_1 &\neq 0, \end{align} \]

since if \(\beta_1=0\) then the model reduces to \(Y = \beta_0 + \epsilon\), and \(X\) and \(Y\) are not associated.

p-values

• To test the null hypothesis, we compute something called a t-statistic (a bell-shaped distribution¹)
• Using statistical software, it is easy to compute the probability of observing any value equal to \(\mid t \mid\) or larger.
• We call this probability the p-value.
• If the p-value is less than some pre-specified level of significance, say \(\alpha = 0.05\), then we reject the null hypothesis in favor of the alternative hypothesis.

1. 🤔 How are the t-distribution and the Normal distribution related? Check this link to find out.

Multivariate linear regression

Let’s fit a multivariate linear regression model to the data in our case study:

# Fit a linear model
df_vars_only <- df %>% 
  select(DP_decide_health_p, all_of(independent_variables))
model <- lm(DP_decide_health_p ~ ., data=df_vars_only)

# To get the summary of the model in a tidy format
library(broom)

# Get the summary of the model
summary(model) %>% broom::tidy()

All variables came back significant:

term	estimate	std.error	t-statistic	p.value
(Intercept)	-6.1849636	1.5599988	-3.964723	7.46e-05
ED_attainment_primary_completed_p	-0.3795206	0.0237743	-15.963477	0.00e+00
ED_attainment_primary_p	0.3493246	0.0162901	21.444025	0.00e+00
ED_educ_years_mean	3.3499834	0.1033276	32.420996	0.00e+00
EI_radio_p	0.1810524	0.0094161	19.227987	0.00e+00
HH_floor_high_p	-0.1317147	0.0139954	-9.411297	0.00e+00
WL_wealth_gini	-13.1988160	2.3530192	-5.609311	0.00e+00
WL_wealth_mean	0.1607037	0.0246131	6.529185	0.00e+00

The model’s equation

\[\begin{align} \operatorname{DP\_decide\_health\_p} = & - 0.38 \times \operatorname{ED\_attainment\_primary\_completed\_p} \\ & + 0.35 \times \operatorname{ED\_attainment\_primary\_p}\\ & + 3.35 \times \operatorname{ED\_educ\_years\_mean}\\ & + 0.18 \times \operatorname{EI\_radio\_p} \\ & - 0.13 \times \operatorname{HH\_floor\_high\_p} \\ & - 13.20 \times \operatorname{WL\_wealth\_gini} \\ & + 0.16 \times \operatorname{WL\_wealth\_mean} \\ & - 6.18 \end{align}\]

🤔 How should we interpret the coefficients this time?

What can go wrong?

• The model is only as good as the data you use to fit it.
• The model is only as good as the assumptions it makes.
• People forget that the level of statistical significance is somewhat arbitrary.

Indicative reading of the week:

Now for something (slightly) different

• RCTs
• A/B testing
• Causal inference

Randomised controlled trials

• A randomised controlled trial (RCT) is a type of experiment in which participants are randomly assigned to one of two or more groups (treatment and control).
• It is the norm in medicine and the life sciences, but also very common in the social sciences.
• It is deemed by some to be the gold standard for determining causality.

RCTs: how do they work?

You have a group of people

• Half of them get a pill
• The other half gets a placebo (sugar pill)

You split them into two groups at random

Then what?

• After a while, you measure the outcome of interest
• You compare the two groups using a statistical hypothesis test
• If the difference is statistically significant, you can conclude that the treatment caused the outcome

A/B testing

Causal Inference

📗 Book recommendation:

Pearl, Judea, and Dana Mackenzie. 2018. The Book of Why: The New Science of Cause and Effect. London: Allen Lane.

–(Pearl and Mackenzie 2018)

References

Aschwanden, Christie. 2015. “Science Isn’t Broken.” FiveThirtyEight. https://fivethirtyeight.com/features/science-isnt-broken/.

Belmin, Camille, Roman Hoffmann, Mahmoud Elkasabi, and Peter-Paul Pichler. 2022a. “LivWell: A Sub-National Database on the Living Conditions of Women and Their Well-Being for 52 Countries.” Zenodo. https://doi.org/10.5281/ZENODO.7277104.

———. 2022b. “LivWell: A Sub-National Dataset on the Living Conditions of Women and Their Well-Being for 52 Countries.” Scientific Data 9 (1): 719. https://doi.org/10.1038/s41597-022-01824-2.

ggcorrplot. 2022. “Visualization of a Correlation Matrix Using Ggplot2.” Visualization of a Correlation Matrix Using Ggplot2. https://rpkgs.datanovia.com/ggcorrplot/.

Pearl, Judea, and Dana Mackenzie. 2018. The Book of Why: The New Science of Cause and Effect. London: Allen Lane.